SymNMF-Net for The Symmetric NMF Problem
Paper and Code
May 26, 2022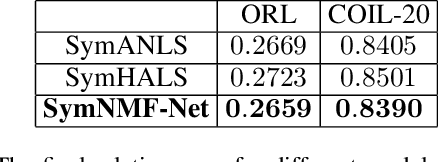
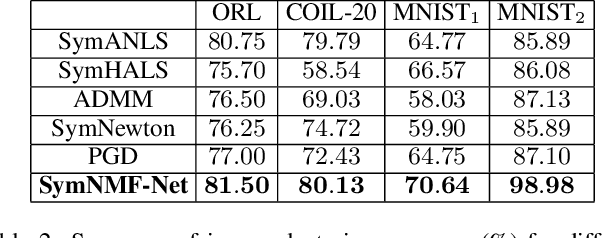
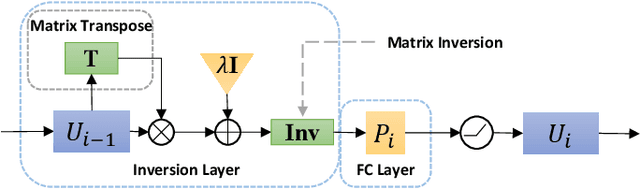
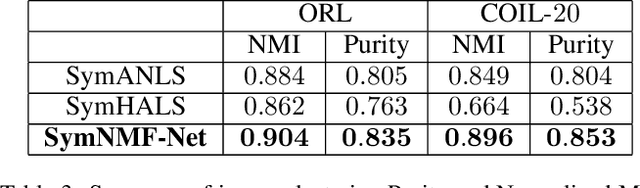
Recently, many works have demonstrated that Symmetric Non-negative Matrix Factorization~(SymNMF) enjoys a great superiority for various clustering tasks. Although the state-of-the-art algorithms for SymNMF perform well on synthetic data, they cannot consistently obtain satisfactory results with desirable properties and may fail on real-world tasks like clustering. Considering the flexibility and strong representation ability of the neural network, in this paper, we propose a neural network called SymNMF-Net for the Symmetric NMF problem to overcome the shortcomings of traditional optimization algorithms. Each block of SymNMF-Net is a differentiable architecture with an inversion layer, a linear layer and ReLU, which are inspired by a traditional update scheme for SymNMF. We show that the inference of each block corresponds to a single iteration of the optimization. Furthermore, we analyze the constraints of the inversion layer to ensure the output stability of the network to a certain extent. Empirical results on real-world datasets demonstrate the superiority of our SymNMF-Net and confirm the sufficiency of our theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge