Successive Pruning for Model Compression via Rate Distortion Theory

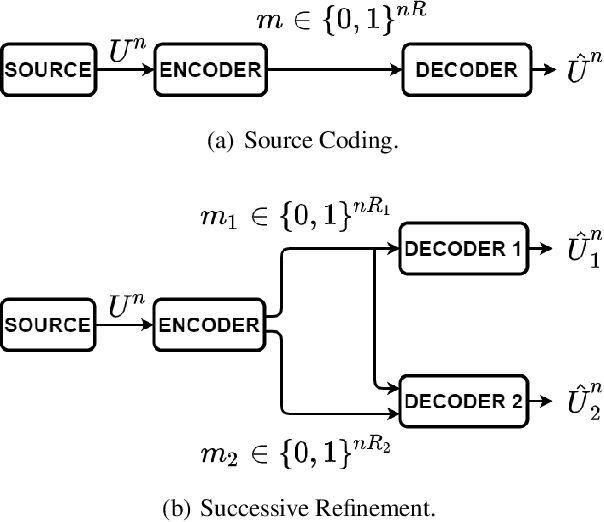
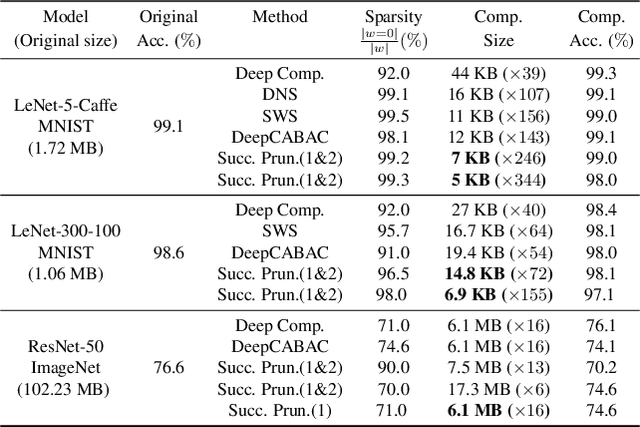
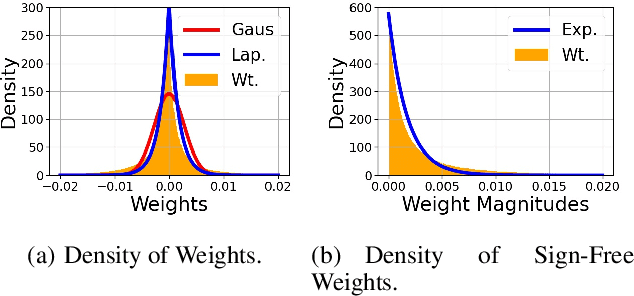
Neural network (NN) compression has become essential to enable deploying over-parameterized NN models on resource-constrained devices. As a simple and easy-to-implement method, pruning is one of the most established NN compression techniques. Although it is a mature method with more than 30 years of history, there is still a lack of good understanding and systematic analysis of why pruning works well even with aggressive compression ratios. In this work, we answer this question by studying NN compression from an information-theoretic approach and show that rate distortion theory suggests pruning to achieve the theoretical limits of NN compression. Our derivation also provides an end-to-end compression pipeline involving a novel pruning strategy. That is, in addition to pruning the model, we also find a minimum-length binary representation of it via entropy coding. Our method consistently outperforms the existing pruning strategies and reduces the pruned model's size by 2.5 times. We evaluate the efficacy of our strategy on MNIST, CIFAR-10 and ImageNet datasets using 5 distinct architectures.