Successive Convex Approximation Based Off-Policy Optimization for Constrained Reinforcement Learning
Paper and Code
May 26, 2021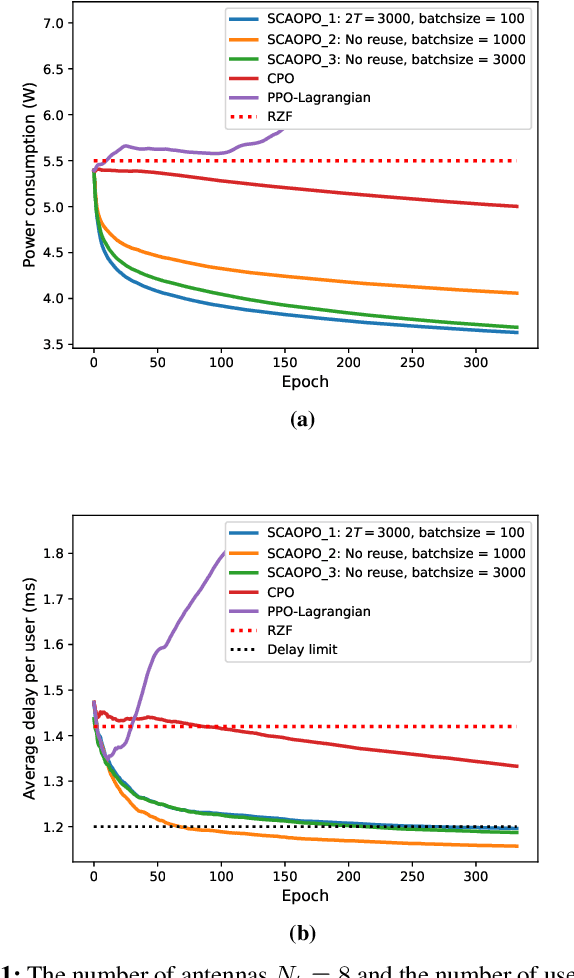
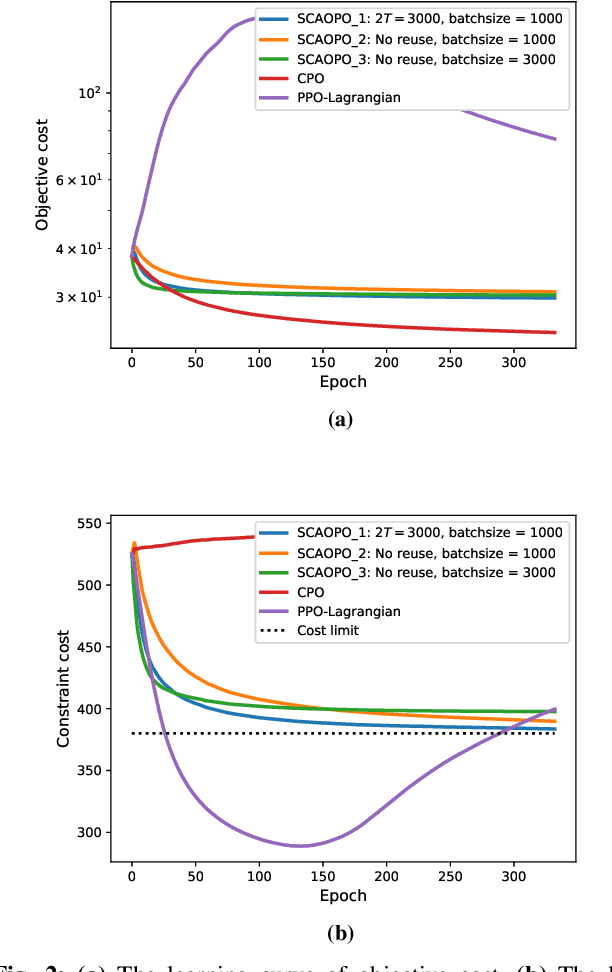
We propose a successive convex approximation based off-policy optimization (SCAOPO) algorithm to solve the general constrained reinforcement learning problem, which is formulated as a constrained Markov decision process (CMDP) in the context of average cost. The SCAOPO is based on solving a sequence of convex objective/feasibility optimization problems obtained by replacing the objective and constraint functions in the original problems with convex surrogate functions. At each iteration, the convex surrogate problem can be efficiently solved by Lagrange dual method even the policy is parameterized by a high-dimensional function. Moreover, the SCAOPO enables to reuse old experiences from previous updates, thereby significantly reducing the implementation cost when deployed in the real-world engineering systems that need to online learn the environment. In spite of the time-varying state distribution and the stochastic bias incurred by the off-policy learning, the SCAOPO with a feasible initial point can still provably converge to a Karush-Kuhn-Tucker (KKT) point of the original problem almost surely.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge