Successfully Applying the Stabilized Lottery Ticket Hypothesis to the Transformer Architecture

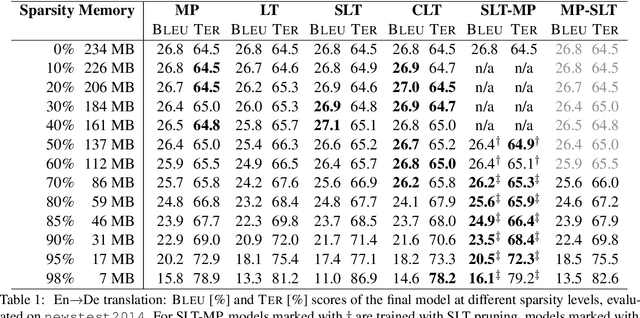
Sparse models require less memory for storage and enable a faster inference by reducing the necessary number of FLOPs. This is relevant both for time-critical and on-device computations using neural networks. The stabilized lottery ticket hypothesis states that networks can be pruned after none or few training iterations, using a mask computed based on the unpruned converged model. On the transformer architecture and the WMT 2014 English-to-German and English-to-French tasks, we show that stabilized lottery ticket pruning performs similar to magnitude pruning for sparsity levels of up to 85%, and propose a new combination of pruning techniques that outperforms all other techniques for even higher levels of sparsity. Furthermore, we confirm that the parameter's initial sign and not its specific value is the primary factor for successful training, and show that magnitude pruning cannot be used to find winning lottery tickets.