Subjective Logic Operators in Trust Assessment: an Empirical Study
Paper and Code
Nov 19, 2013
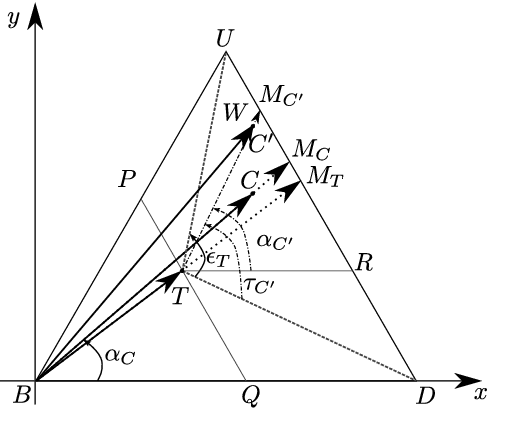
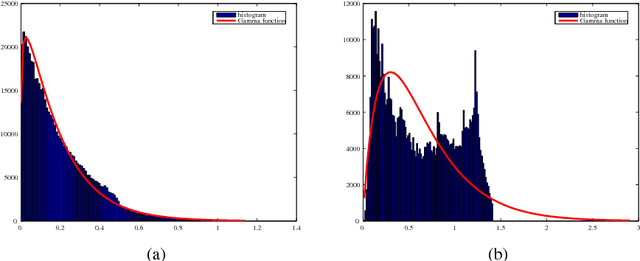
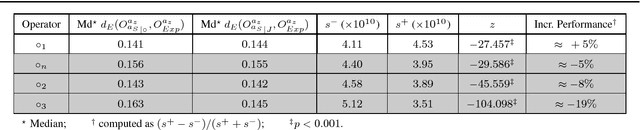
Computational trust mechanisms aim to produce trust ratings from both direct and indirect information about agents' behaviour. Subjective Logic (SL) has been widely adopted as the core of such systems via its fusion and discount operators. In recent research we revisited the semantics of these operators to explore an alternative, geometric interpretation. In this paper we present a principled desiderata for discounting and fusion operators in SL. Building upon this we present operators that satisfy these desirable properties, including a family of discount operators. We then show, through a rigorous empirical study, that specific, geometrically interpreted operators significantly outperform standard SL operators in estimating ground truth. These novel operators offer real advantages for computational models of trust and reputation, in which they may be employed without modifying other aspects of an existing system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge