Sub-Optimal Local Minima Exist for Almost All Over-parameterized Neural Networks

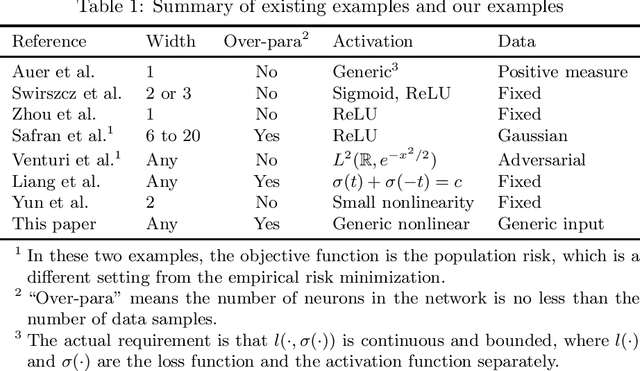
Does over-parameterization eliminate sub-optimal local minima for neural network problems? On one hand, existing positive results do not prove the claim, but often weaker claims. On the other hand, existing negative results have strong assumptions on the activation functions and/or data samples, causing a large gap with positive results. It was unclear before whether there is a clean answer of "yes" or "no". In this paper, we answer this question with a strong negative result. In particular, we prove that for deep and over-parameterized networks, sub-optimal local minima exist for generic input data samples and generic nonlinear activation. This is the setting widely studied in the global landscape of over-parameterized networks, thus our result corrects a possible misconception that "over-parameterization eliminates sub-optimal local-min". Our construction is based on fundamental optimization analysis, and thus rather principled.