Structured Prediction of Sequences and Trees using Infinite Contexts
Paper and Code
Mar 09, 2015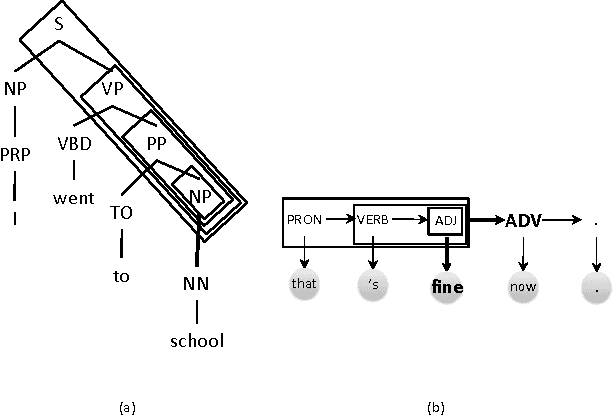
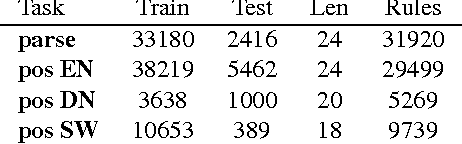
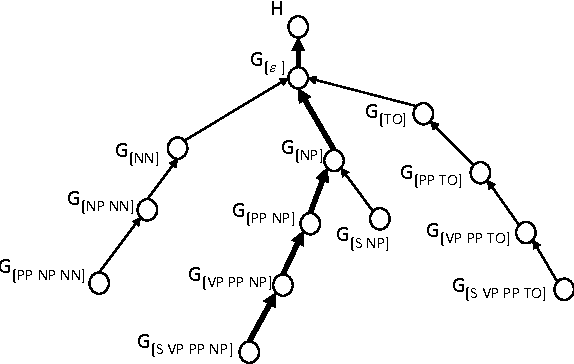
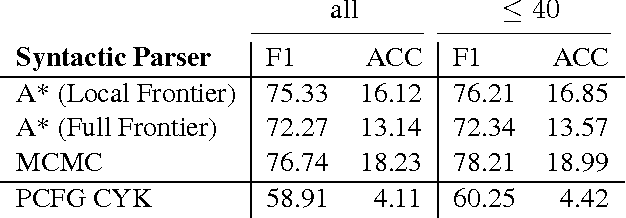
Linguistic structures exhibit a rich array of global phenomena, however commonly used Markov models are unable to adequately describe these phenomena due to their strong locality assumptions. We propose a novel hierarchical model for structured prediction over sequences and trees which exploits global context by conditioning each generation decision on an unbounded context of prior decisions. This builds on the success of Markov models but without imposing a fixed bound in order to better represent global phenomena. To facilitate learning of this large and unbounded model, we use a hierarchical Pitman-Yor process prior which provides a recursive form of smoothing. We propose prediction algorithms based on A* and Markov Chain Monte Carlo sampling. Empirical results demonstrate the potential of our model compared to baseline finite-context Markov models on part-of-speech tagging and syntactic parsing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge