Structural Entropy Guided Graph Hierarchical Pooling
Paper and Code
Jun 26, 2022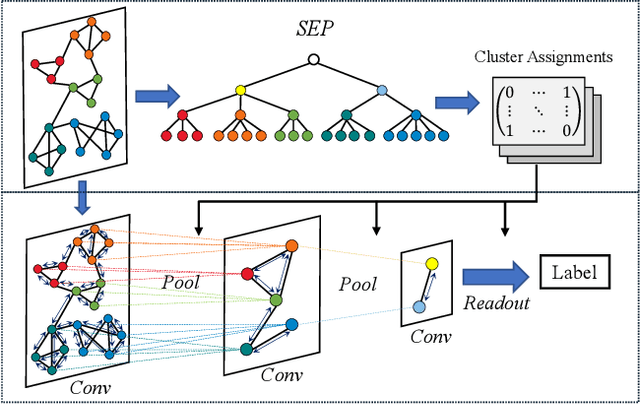



Following the success of convolution on non-Euclidean space, the corresponding pooling approaches have also been validated on various tasks regarding graphs. However, because of the fixed compression quota and stepwise pooling design, these hierarchical pooling methods still suffer from local structure damage and suboptimal problem. In this work, inspired by structural entropy, we propose a hierarchical pooling approach, SEP, to tackle the two issues. Specifically, without assigning the layer-specific compression quota, a global optimization algorithm is designed to generate the cluster assignment matrices for pooling at once. Then, we present an illustration of the local structure damage from previous methods in the reconstruction of ring and grid synthetic graphs. In addition to SEP, we further design two classification models, SEP-G and SEP-N for graph classification and node classification, respectively. The results show that SEP outperforms state-of-the-art graph pooling methods on graph classification benchmarks and obtains superior performance on node classifications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge