Structural Design Using Laplacian Shells
Paper and Code
Jun 25, 2019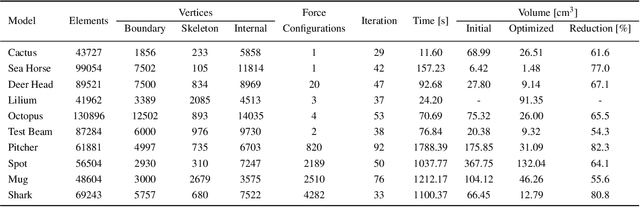
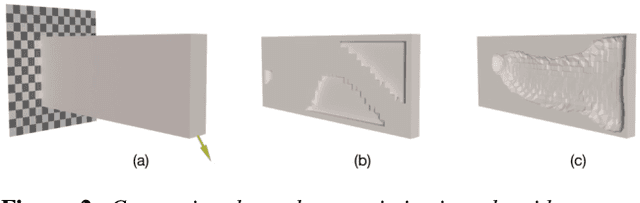

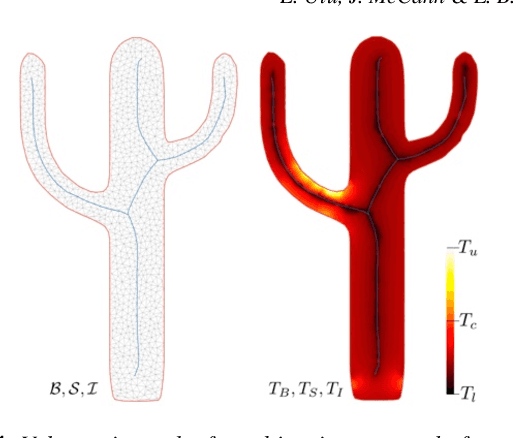
We introduce a method to design lightweight shell objects that are structurally robust under the external forces they may experience during use. Given an input 3D model and a general description of the external forces, our algorithm generates a structurally-sound minimum weight shell object. Our approach works by altering the local shell thickness repeatedly based on the stresses that develop inside the object. A key issue in shell design is that large thickness values might result in self-intersections on the inner boundary creating a significant computational challenge during optimization. To address this, we propose a shape parametrization based on the solution to the Laplace's equation that guarantees smooth and intersection-free shell boundaries. Combined with our gradient-free optimization algorithm, our method provides a practical solution to the structural design of hollow objects with a single inner cavity. We demonstrate our method on a variety of problems with arbitrary 3D models under complex force configurations and validate its performance with physical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge