Streaming PAC-Bayes Gaussian process regression with a performance guarantee for online decision making
Paper and Code
Oct 16, 2022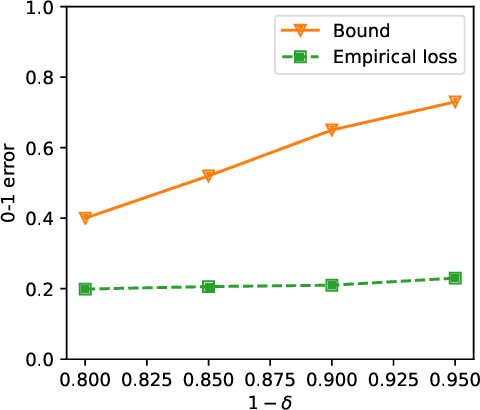

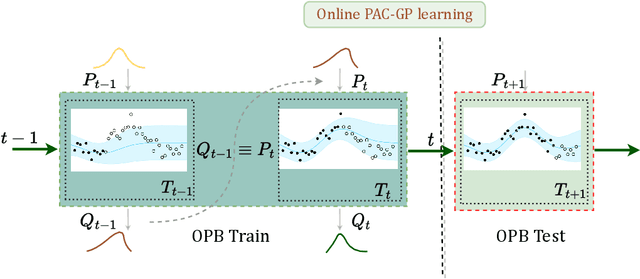
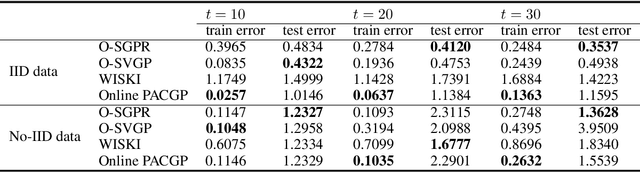
As a powerful Bayesian non-parameterized algorithm, the Gaussian process (GP) has performed a significant role in Bayesian optimization and signal processing. GPs have also advanced online decision-making systems because their posterior distribution has a closed-form solution. However, its training and inference process requires all historic data to be stored and the GP model to be trained from scratch. For those reasons, several online GP algorithms, such as O-SGPR and O-SVGP, have been specifically designed for streaming settings. In this paper, we present a new theoretical framework for online GPs based on the online probably approximately correct (PAC) Bayes theory. The framework offers both a guarantee of generalized performance and good accuracy. Instead of minimizing the marginal likelihood, our algorithm optimizes both the empirical risk function and a regularization item, which is in proportion to the divergence between the prior distribution and posterior distribution of parameters. In addition to its theoretical appeal, the algorithm performs well empirically on several regression datasets. Compared to other online GP algorithms, ours yields a generalization guarantee and very competitive accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge