Storchastic: A Framework for General Stochastic Automatic Differentiation
Paper and Code
Apr 01, 2021

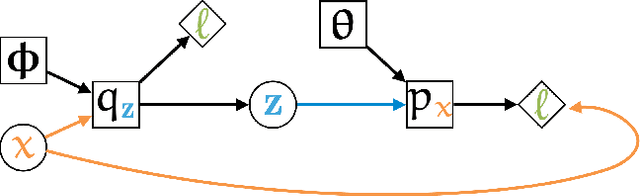

Modelers use automatic differentiation of computation graphs to implement complex Deep Learning models without defining gradient computations. However, modelers often use sampling methods to estimate intractable expectations such as in Reinforcement Learning and Variational Inference. Current methods for estimating gradients through these sampling steps are limited: They are either only applicable to continuous random variables and differentiable functions, or can only use simple but high variance score-function estimators. To overcome these limitations, we introduce Storchastic, a new framework for automatic differentiation of stochastic computation graphs. Storchastic allows the modeler to choose from a wide variety of gradient estimation methods at each sampling step, to optimally reduce the variance of the gradient estimates. Furthermore, Storchastic is provably unbiased for estimation of any-order gradients, and generalizes variance reduction techniques to higher-order gradient estimates. Finally, we implement Storchastic as a PyTorch library.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge