Stochastically Dominant Distributional Reinforcement Learning

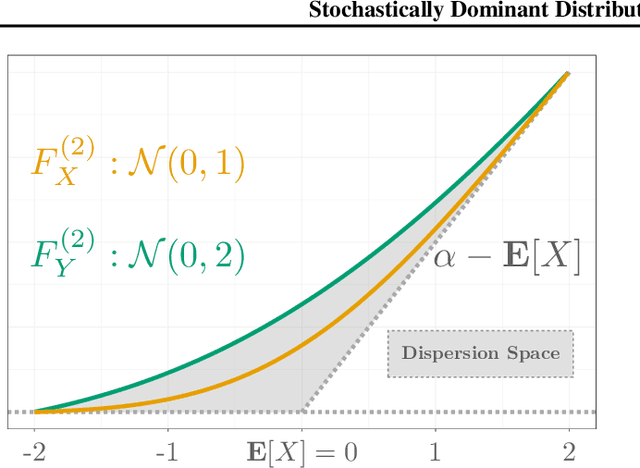
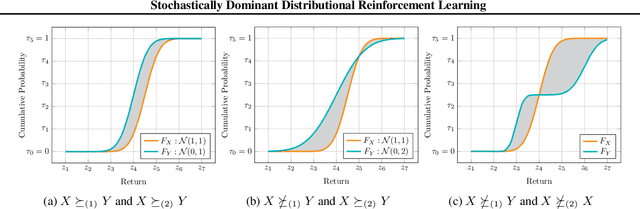
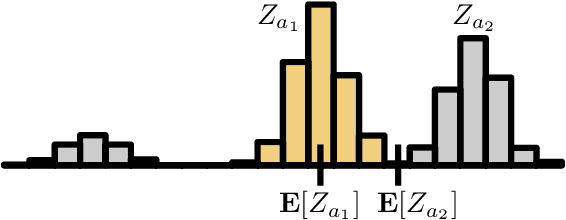
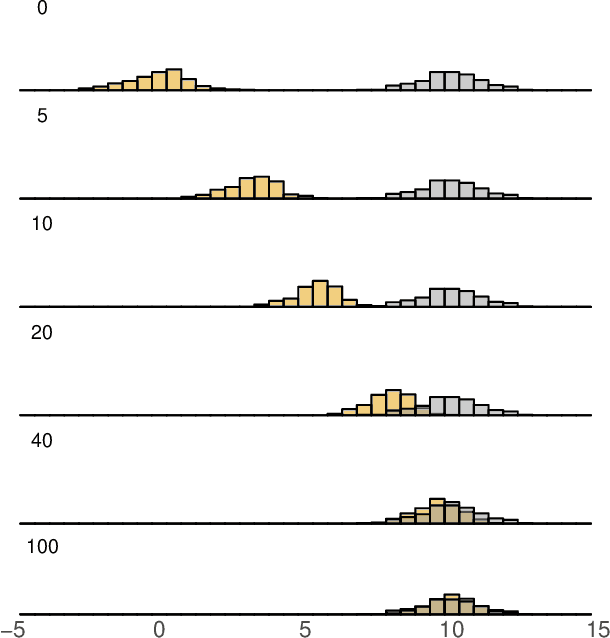
We describe a new approach for mitigating risk in the Reinforcement Learning paradigm. Instead of reasoning about expected utility, we use second-order stochastic dominance (SSD) to directly compare the inherent risk of random returns induced by different actions. We frame the RL optimization within the space of probability measures to accommodate the SSD relation, treating Bellman's equation as a potential energy functional. This brings us to Wasserstein gradient flows, for which the optimality and convergence are well understood. We propose a discrete-measure approximation algorithm called the Dominant Particle Agent (DPA), and we demonstrate how safety and performance are better balanced with DPA than with existing baselines.