Stochastic Weight Averaging Revisited

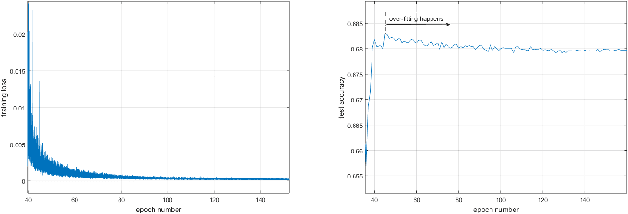
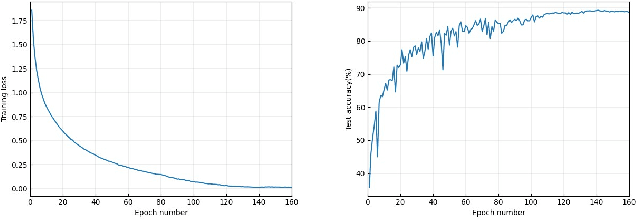
Stochastic weight averaging (SWA) is recognized as a simple while one effective approach to improve the generalization of stochastic gradient descent (SGD) for training deep neural networks (DNNs). A common insight to explain its success is that averaging weights following an SGD process equipped with cyclical or high constant learning rates can discover wider optima, which then lead to better generalization. We give a new insight that does not concur with the above one. We characterize that SWA's performance is highly dependent on to what extent the SGD process that runs before SWA converges, and the operation of weight averaging only contributes to variance reduction. This new insight suggests practical guides on better algorithm design. As an instantiation, we show that following an SGD process with insufficient convergence, running SWA more times leads to continual incremental benefits in terms of generalization. Our findings are corroborated by extensive experiments across different network architectures, including a baseline CNN, PreResNet-164, WideResNet-28-10, VGG16, ResNet-50, ResNet-152, DenseNet-161, and different datasets including CIFAR-{10,100}, and Imagenet.