Stochastic Semi-Gradient Descent for Learning Mean Field Games with Population-Aware Function Approximation
Paper and Code
Aug 15, 2024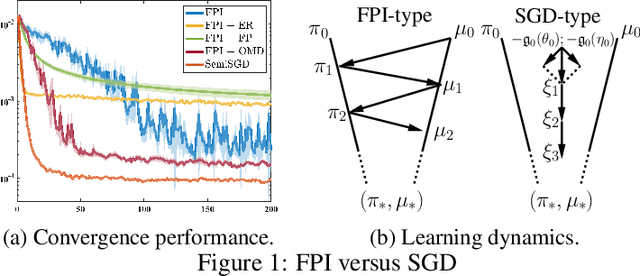

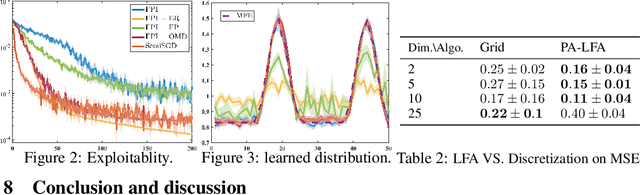

Mean field games (MFGs) model the interactions within a large-population multi-agent system using the population distribution. Traditional learning methods for MFGs are based on fixed-point iteration (FPI), which calculates best responses and induced population distribution separately and sequentially. However, FPI-type methods suffer from inefficiency and instability, due to oscillations caused by the forward-backward procedure. This paper considers an online learning method for MFGs, where an agent updates its policy and population estimates simultaneously and fully asynchronously, resulting in a simple stochastic gradient descent (SGD) type method called SemiSGD. Not only does SemiSGD exhibit numerical stability and efficiency, but it also provides a novel perspective by treating the value function and population distribution as a unified parameter. We theoretically show that SemiSGD directs this unified parameter along a descent direction to the mean field equilibrium. Motivated by this perspective, we develop a linear function approximation (LFA) for both the value function and the population distribution, resulting in the first population-aware LFA for MFGs on continuous state-action space. Finite-time convergence and approximation error analysis are provided for SemiSGD equipped with population-aware LFA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge