Stochastic Distributed Optimization for Machine Learning from Decentralized Features
Paper and Code
Dec 16, 2018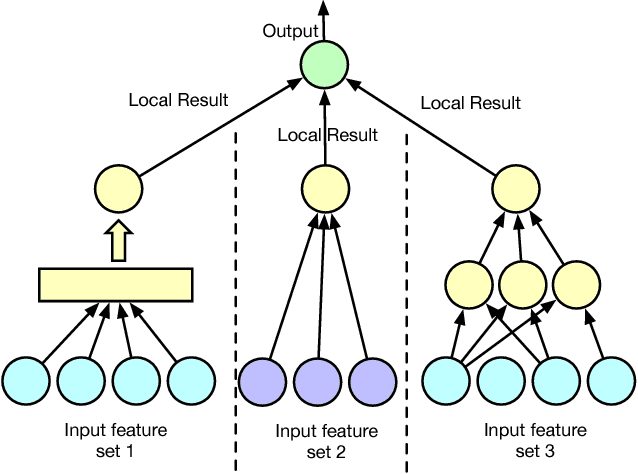


Distributed machine learning has been widely studied in the literature to scale up machine learning model training in the presence of an ever-increasing amount of data. We study distributed machine learning from another perspective, where the information about the training same samples are inherently decentralized and located on different parities. We propose an asynchronous stochastic gradient descent (SGD) algorithm for such a feature distributed machine learning (FDML) problem, to jointly learn from decentralized features, with theoretical convergence guarantees under bounded asynchrony. Our algorithm does not require sharing the original feature data or even local model parameters between parties, thus preserving a high level of data confidentiality. We implement our algorithm for FDML in a parameter server architecture. We compare our system with fully centralized training (which violates data locality requirements) and training only based on local features, through extensive experiments performed on a large amount of data from a real-world application, involving 5 million samples and $8700$ features in total. Experimental results have demonstrated the effectiveness and efficiency of the proposed FDML system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge