Stochastic Beams and Where to Find Them: The Gumbel-Top-k Trick for Sampling Sequences Without Replacement
Paper and Code
Mar 14, 2019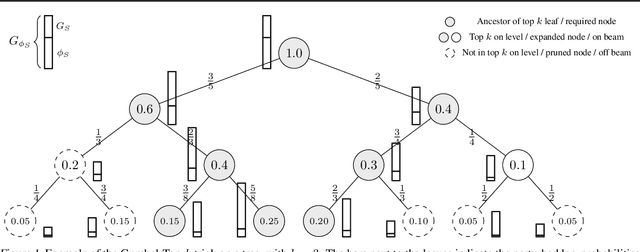
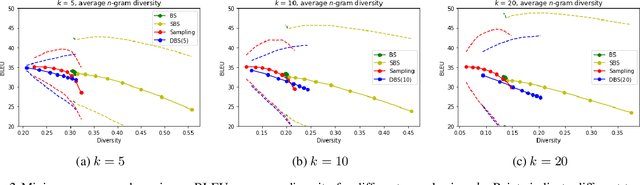
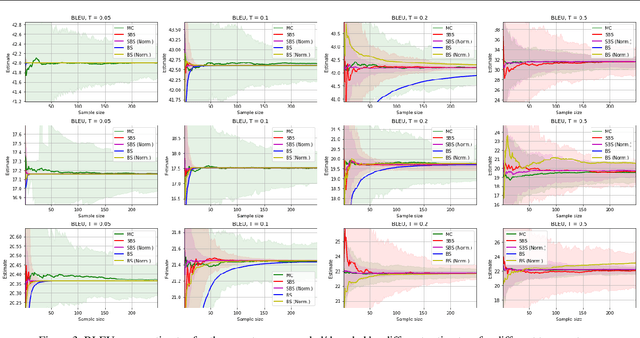
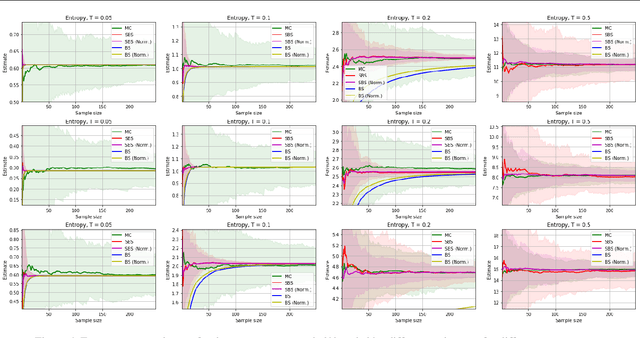
The well-known Gumbel-Max trick for sampling from a categorical distribution can be extended to sample $k$ elements without replacement. We show how to implicitly apply this 'Gumbel-Top-$k$' trick on a factorized distribution over sequences, allowing to draw exact samples without replacement using a Stochastic Beam Search. Even for exponentially large domains, the number of model evaluations grows only linear in $k$ and the maximum sampled sequence length. The algorithm creates a theoretical connection between sampling and (deterministic) beam search and can be used as a principled intermediate alternative. In a translation task, the proposed method compares favourably against alternatives to obtain diverse yet good quality translations. We show that sequences sampled without replacement can be used to construct low-variance estimators for expected sentence-level BLEU score and model entropy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge