Statistically Robust Neural Network Classification
Paper and Code
Dec 11, 2019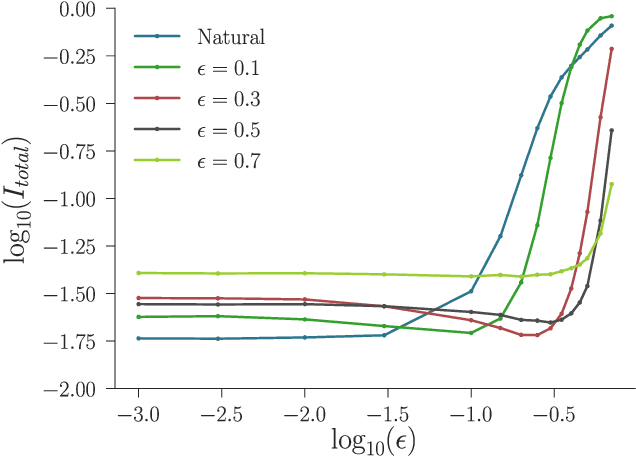
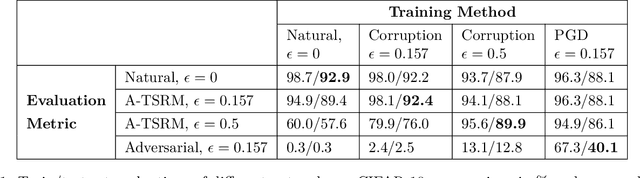
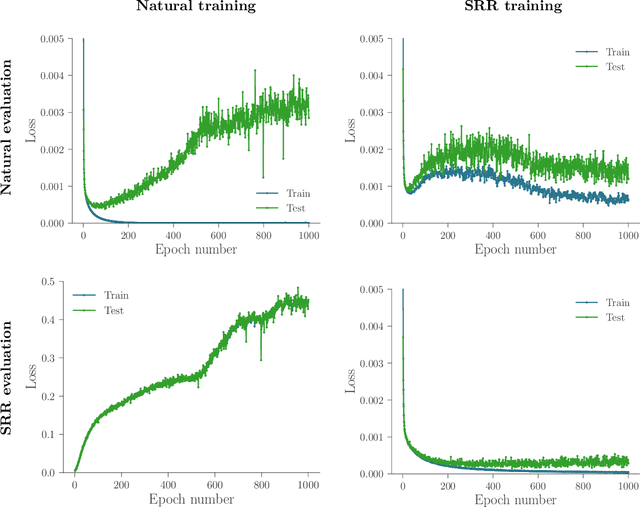
Recently there has been much interest in quantifying the robustness of neural network classifiers through adversarial risk metrics. However, for problems where test-time corruptions occur in a probabilistic manner, rather than being generated by an explicit adversary, adversarial metrics typically do not provide an accurate or reliable indicator of robustness. To address this, we introduce a statistically robust risk (SRR) framework which measures robustness in expectation over both network inputs and a corruption distribution. Unlike many adversarial risk metrics, which typically require separate applications on a point-by-point basis, the SRR can easily be directly estimated for an entire network and used as a training objective in a stochastic gradient scheme. Furthermore, we show both theoretically and empirically that it can scale to higher-dimensional networks by providing superior generalization performance compared with comparable adversarial risks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge