Stacked Quantizers for Compositional Vector Compression
Paper and Code
Nov 08, 2014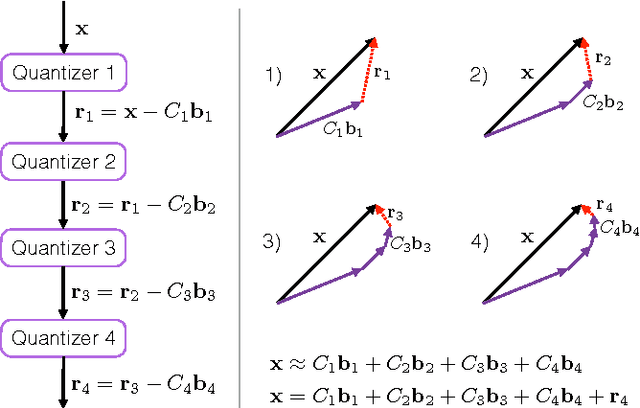
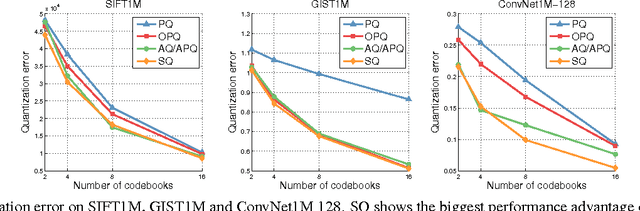
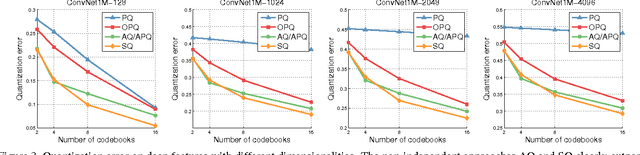
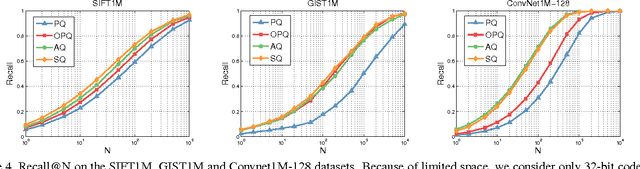
Recently, Babenko and Lempitsky introduced Additive Quantization (AQ), a generalization of Product Quantization (PQ) where a non-independent set of codebooks is used to compress vectors into small binary codes. Unfortunately, under this scheme encoding cannot be done independently in each codebook, and optimal encoding is an NP-hard problem. In this paper, we observe that PQ and AQ are both compositional quantizers that lie on the extremes of the codebook dependence-independence assumption, and explore an intermediate approach that exploits a hierarchical structure in the codebooks. This results in a method that achieves quantization error on par with or lower than AQ, while being several orders of magnitude faster. We perform a complexity analysis of PQ, AQ and our method, and evaluate our approach on standard benchmarks of SIFT and GIST descriptors, as well as on new datasets of features obtained from state-of-the-art convolutional neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge