Stack operation of tensor networks
Paper and Code
Mar 28, 2022
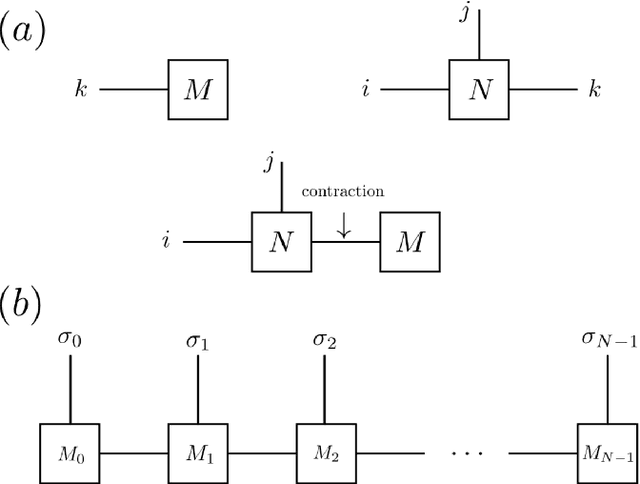
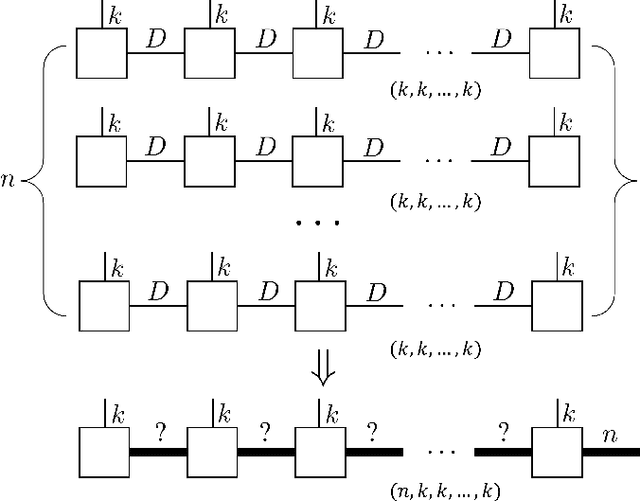
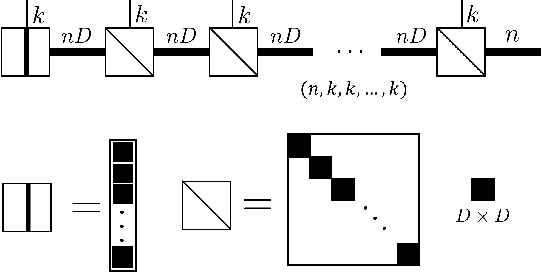
The tensor network, as a facterization of tensors, aims at performing the operations that are common for normal tensors, such as addition, contraction and stacking. However, due to its non-unique network structure, only the tensor network contraction is so far well defined. In this paper, we propose a mathematically rigorous definition for the tensor network stack approach, that compress a large amount of tensor networks into a single one without changing their structures and configurations. We illustrate the main ideas with the matrix product states based machine learning as an example. Our results are compared with the for loop and the efficient coding method on both CPU and GPU.
* 9 pages, 10 figures, for the code on Github, see this
https://github.com/veya2ztn/Stack_of_Tensor_Network
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge