Stable Training of Probabilistic Models Using the Leave-One-Out Maximum Log-Likelihood Objective

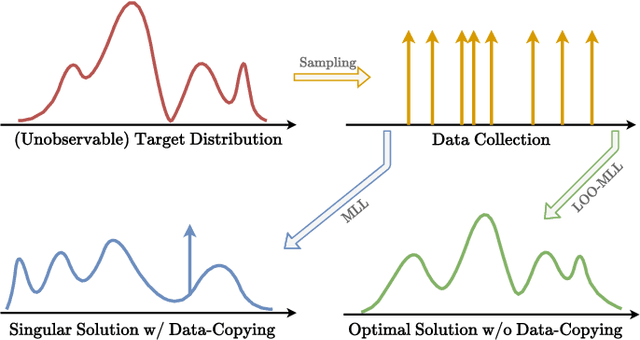
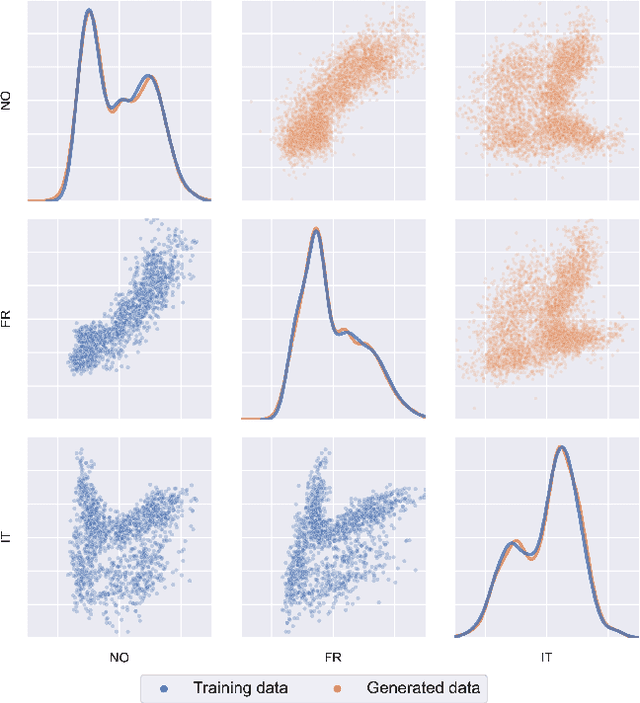
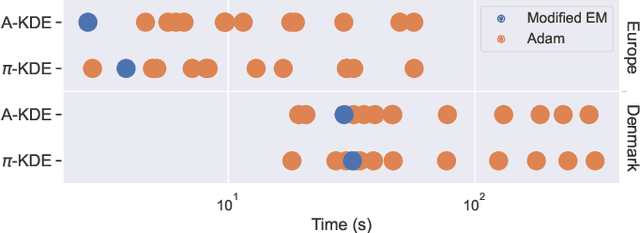
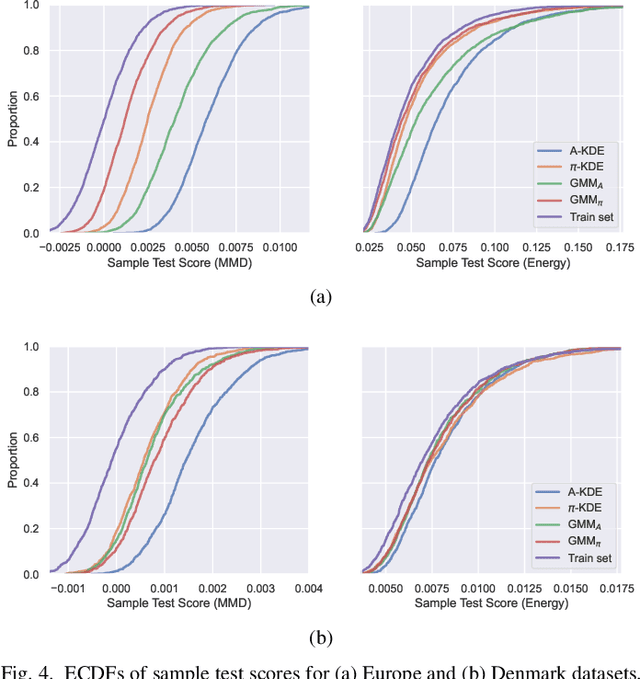
Probabilistic modelling of power systems operation and planning processes depends on data-driven methods, which require sufficiently large datasets. When historical data lacks this, it is desired to model the underlying data generation mechanism as a probability distribution to assess the data quality and generate more data, if needed. Kernel density estimation (KDE) based models are popular choices for this task, but they fail to adapt to data regions with varying densities. In this paper, an adaptive KDE model is employed to circumvent this, where each kernel in the model has an individual bandwidth. The leave-one-out maximum log-likelihood (LOO-MLL) criterion is proposed to prevent the singular solutions that the regular MLL criterion gives rise to, and it is proven that LOO-MLL prevents these. Relying on this guaranteed robustness, the model is extended by assigning learnable weights to the kernels. In addition, a modified expectation-maximization algorithm is employed to accelerate the optimization speed reliably. The performance of the proposed method and models are exhibited on two power systems datasets using different statistical tests and by comparison with Gaussian mixture models. Results show that the proposed models have promising performance, in addition to their singularity prevention guarantees.