Stability-Certified Reinforcement Learning via Spectral Normalization
Paper and Code
Dec 26, 2020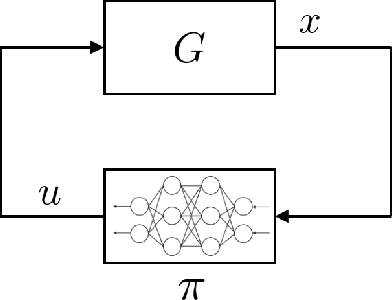
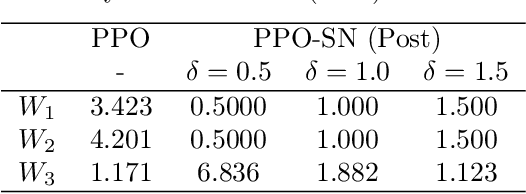
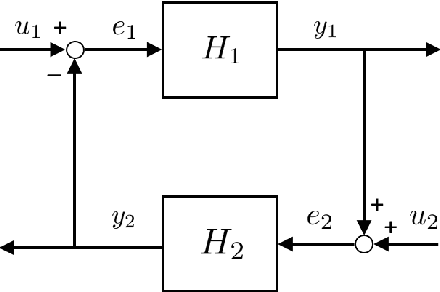

In this article, two types of methods from different perspectives based on spectral normalization are described for ensuring the stability of the system controlled by a neural network. The first one is that the L2 gain of the feedback system is bounded less than 1 to satisfy the stability condition derived from the small-gain theorem. While explicitly including the stability condition, the first method may provide an insufficient performance on the neural network controller due to its strict stability condition. To overcome this difficulty, the second one is proposed, which improves the performance while ensuring the local stability with a larger region of attraction. In the second method, the stability is ensured by solving linear matrix inequalities after training the neural network controller. The spectral normalization proposed in this article improves the feasibility of the a-posteriori stability test by constructing tighter local sectors. The numerical experiments show that the second method provides enough performance compared with the first one while ensuring enough stability compared with the existing reinforcement learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge