Stability and Identification of Random Asynchronous Linear Time-Invariant Systems
Paper and Code
Dec 08, 2020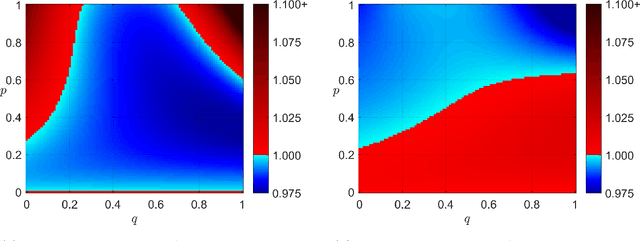

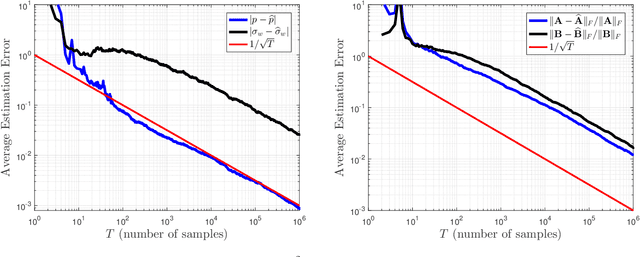
In many computational tasks and dynamical systems, asynchrony and randomization are naturally present and have been considered as ways to increase the speed and reduce the cost of computation while compromising the accuracy and convergence rate. In this work, we show the additional benefits of randomization and asynchrony on the stability of linear dynamical systems. We introduce a natural model for random asynchronous linear time-invariant (LTI) systems which generalizes the standard (synchronous) LTI systems. In this model, each state variable is updated randomly and asynchronously with some probability according to the underlying system dynamics. We examine how the mean-square stability of random asynchronous LTI systems vary with respect to randomization and asynchrony. Surprisingly, we show that the stability of random asynchronous LTI systems does not imply or is not implied by the stability of the synchronous variant of the system and an unstable synchronous system can be stabilized via randomization and/or asynchrony. We further study a special case of the introduced model, namely randomized LTI systems, where each state element is updated randomly with some fixed but unknown probability. We consider the problem of system identification of unknown randomized LTI systems using the precise characterization of mean-square stability via extended Lyapunov equation. For unknown randomized LTI systems, we propose a systematic identification method to recover the underlying dynamics. Given a single input/output trajectory, our method estimates the model parameters that govern the system dynamics, the update probability of state variables, and the noise covariance using the correlation matrices of collected data and the extended Lyapunov equation. Finally, we empirically demonstrate that the proposed method consistently recovers the underlying system dynamics with the optimal rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge