Spike and Slab Gaussian Process Latent Variable Models
Paper and Code
May 10, 2015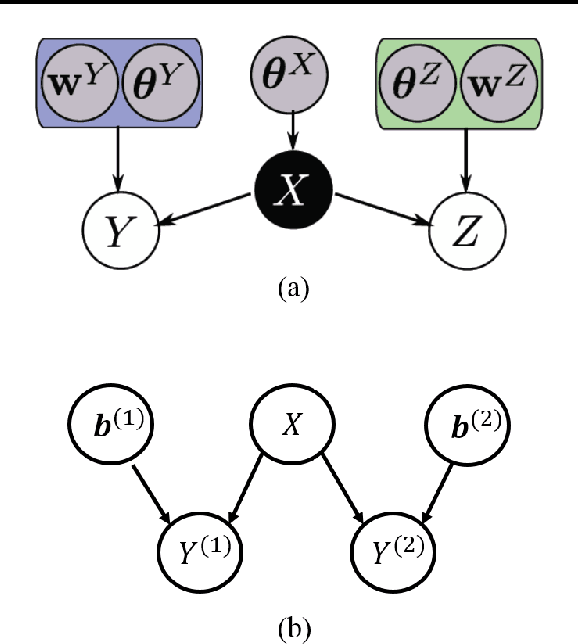
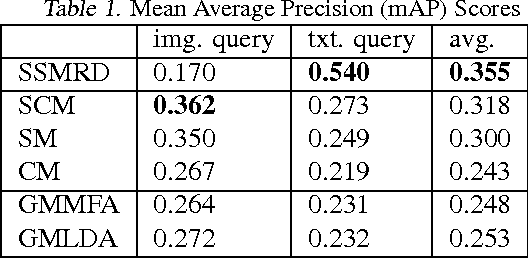

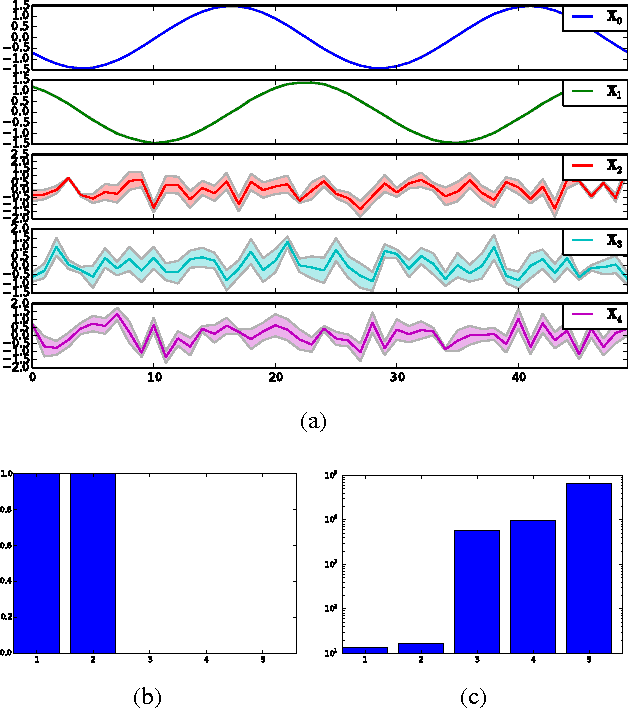
The Gaussian process latent variable model (GP-LVM) is a popular approach to non-linear probabilistic dimensionality reduction. One design choice for the model is the number of latent variables. We present a spike and slab prior for the GP-LVM and propose an efficient variational inference procedure that gives a lower bound of the log marginal likelihood. The new model provides a more principled approach for selecting latent dimensions than the standard way of thresholding the length-scale parameters. The effectiveness of our approach is demonstrated through experiments on real and simulated data. Further, we extend multi-view Gaussian processes that rely on sharing latent dimensions (known as manifold relevance determination) with spike and slab priors. This allows a more principled approach for selecting a subset of the latent space for each view of data. The extended model outperforms the previous state-of-the-art when applied to a cross-modal multimedia retrieval task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge