Speech recognition with quaternion neural networks
Paper and Code
Nov 21, 2018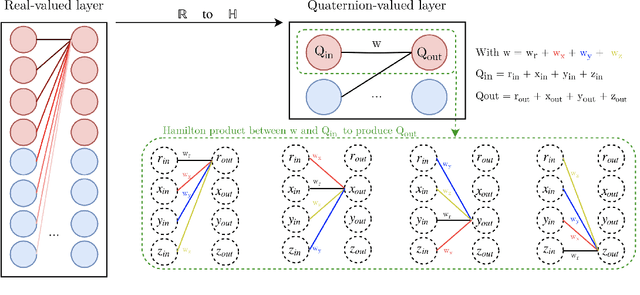


Neural network architectures are at the core of powerful automatic speech recognition systems (ASR). However, while recent researches focus on novel model architectures, the acoustic input features remain almost unchanged. Traditional ASR systems rely on multidimensional acoustic features such as the Mel filter bank energies alongside with the first, and second order derivatives to characterize time-frames that compose the signal sequence. Considering that these components describe three different views of the same element, neural networks have to learn both the internal relations that exist within these features, and external or global dependencies that exist between the time-frames. Quaternion-valued neural networks (QNN), recently received an important interest from researchers to process and learn such relations in multidimensional spaces. Indeed, quaternion numbers and QNNs have shown their efficiency to process multidimensional inputs as entities, to encode internal dependencies, and to solve many tasks with up to four times less learning parameters than real-valued models. We propose to investigate modern quaternion-valued models such as convolutional and recurrent quaternion neural networks in the context of speech recognition with the TIMIT dataset. The experiments show that QNNs always outperform real-valued equivalent models with way less free parameters, leading to a more efficient, compact, and expressive representation of the relevant information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge