Spectral Methods for Nonparametric Models
Paper and Code
Mar 31, 2017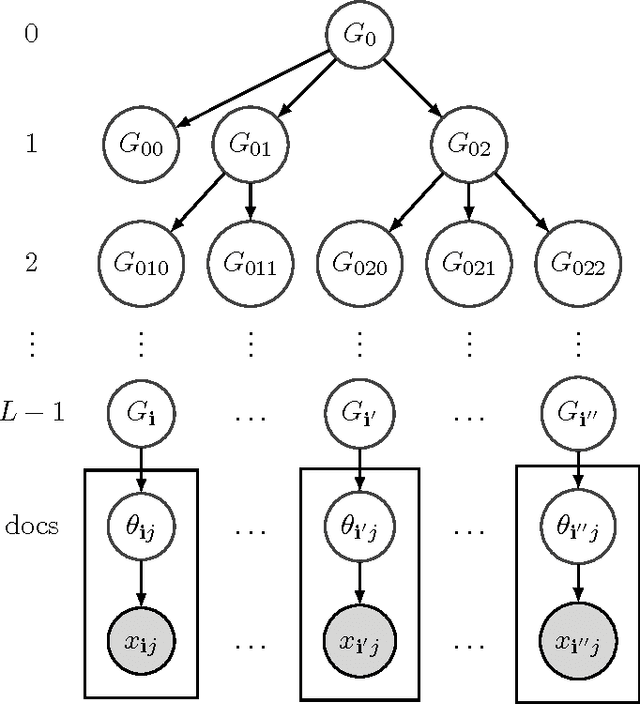

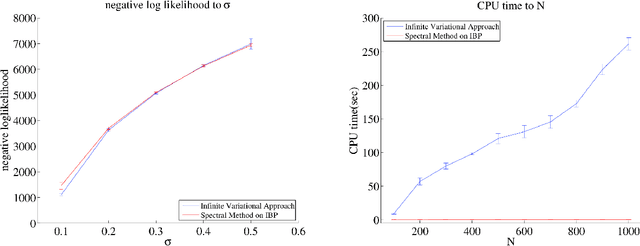

Nonparametric models are versatile, albeit computationally expensive, tool for modeling mixture models. In this paper, we introduce spectral methods for the two most popular nonparametric models: the Indian Buffet Process (IBP) and the Hierarchical Dirichlet Process (HDP). We show that using spectral methods for the inference of nonparametric models are computationally and statistically efficient. In particular, we derive the lower-order moments of the IBP and the HDP, propose spectral algorithms for both models, and provide reconstruction guarantees for the algorithms. For the HDP, we further show that applying hierarchical models on dataset with hierarchical structure, which can be solved with the generalized spectral HDP, produces better solutions to that of flat models regarding likelihood performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge