Spectral Graph Transformer Networks for Brain Surface Parcellation
Paper and Code
Nov 22, 2019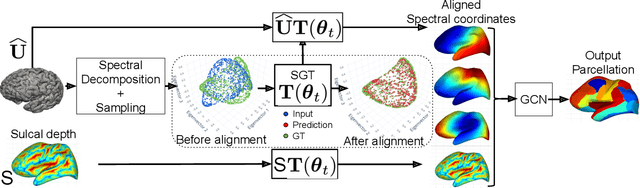
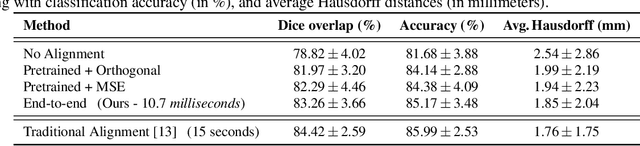
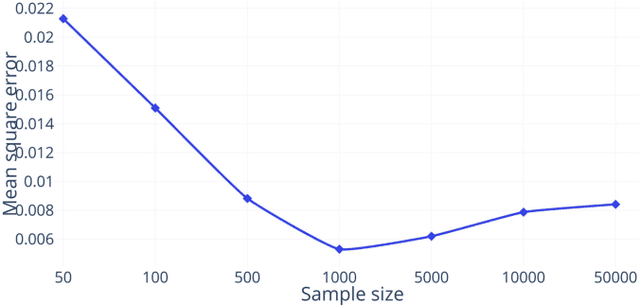
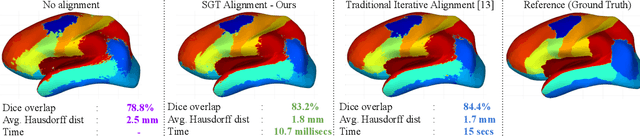
The analysis of the brain surface modeled as a graph mesh is a challenging task. Conventional deep learning approaches often rely on data lying in the Euclidean space. As an extension to irregular graphs, convolution operations are defined in the Fourier or spectral domain. This spectral domain is obtained by decomposing the graph Laplacian, which captures relevant shape information. However, the spectral decomposition across different brain graphs causes inconsistencies between the eigenvectors of individual spectral domains, causing the graph learning algorithm to fail. Current spectral graph convolution methods handle this variance by separately aligning the eigenvectors to a reference brain in a slow iterative step. This paper presents a novel approach for learning the transformation matrix required for aligning brain meshes using a direct data-driven approach. Our alignment and graph processing method provides a fast analysis of brain surfaces. The novel Spectral Graph Transformer (SGT) network proposed in this paper uses very few randomly sub-sampled nodes in the spectral domain to learn the alignment matrix for multiple brain surfaces. We validate the use of this SGT network along with a graph convolution network to perform cortical parcellation. Our method on 101 manually-labeled brain surfaces shows improved parcellation performance over a no-alignment strategy, gaining a significant speed (1400 fold) over traditional iterative alignment approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge