Spectral Graph Matching and Regularized Quadratic Relaxations II: Erdős-Rényi Graphs and Universality

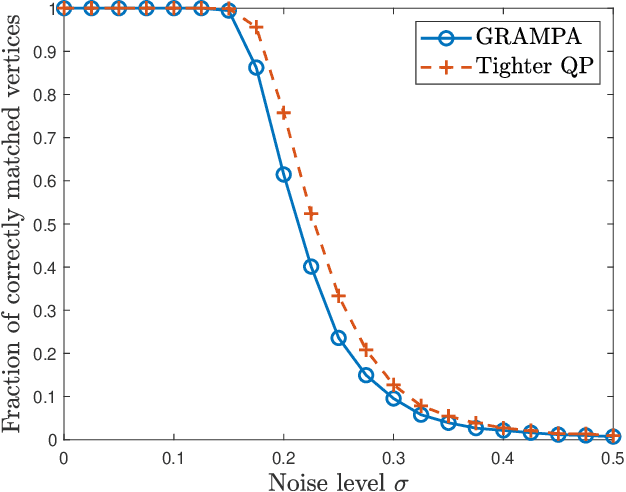
We analyze a new spectral graph matching algorithm, GRAph Matching by Pairwise eigen-Alignments (GRAMPA), for recovering the latent vertex correspondence between two unlabeled, edge-correlated weighted graphs. Extending the exact recovery guarantees established in the companion paper for Gaussian weights, in this work, we prove the universality of these guarantees for a general correlated Wigner model. In particular, for two Erd\H{o}s-R\'enyi graphs with edge correlation coefficient $1-\sigma^2$ and average degree at least $\operatorname{polylog}(n)$, we show that GRAMPA exactly recovers the latent vertex correspondence with high probability when $\sigma \lesssim 1/\operatorname{polylog}(n)$. Moreover, we establish a similar guarantee for a variant of GRAMPA, corresponding to a tighter quadratic programming relaxation of the quadratic assignment problem. Our analysis exploits a resolvent representation of the GRAMPA similarity matrix and local laws for the resolvents of sparse Wigner matrices.