Sparse Representations of Positive Functions via Projected Pseudo-Mirror Descent
Paper and Code
Nov 13, 2020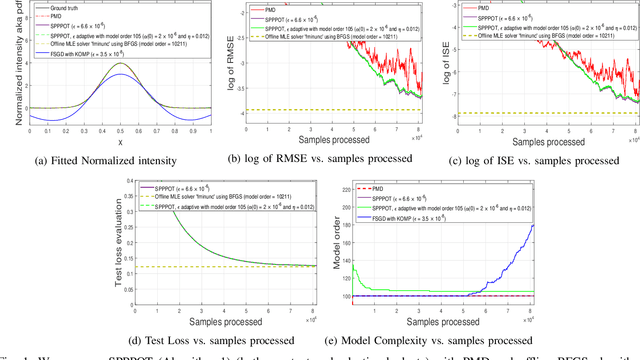
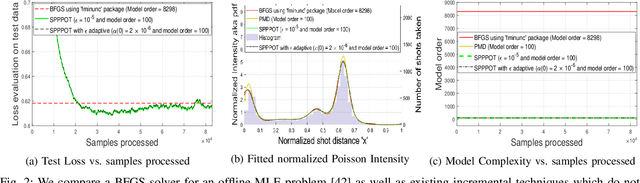
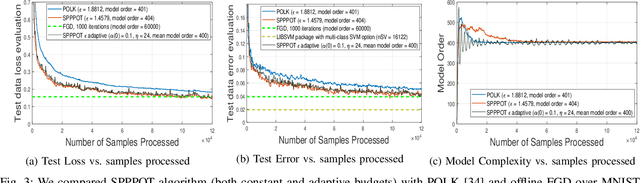
We consider the problem of expected risk minimization when the population loss is strongly convex and the target domain of the decision variable is required to be nonnegative, motivated by the settings of maximum likelihood estimation (MLE) and trajectory optimization. We restrict focus to the case that the decision variable belongs to a nonparametric Reproducing Kernel Hilbert Space (RKHS). To solve it, we consider stochastic mirror descent that employs (i) pseudo-gradients and (ii) projections. Compressive projections are executed via kernel orthogonal matching pursuit (KOMP), and overcome the fact that the vanilla RKHS parameterization grows unbounded with time. Moreover, pseudo-gradients are needed, e.g., when stochastic gradients themselves define integrals over unknown quantities that must be evaluated numerically, as in estimating the intensity parameter of an inhomogeneous Poisson Process, and multi-class kernel logistic regression with latent multi-kernels. We establish tradeoffs between accuracy of convergence in mean and the projection budget parameter under constant step-size and compression budget, as well as non-asymptotic bounds on the model complexity. Experiments demonstrate that we achieve state-of-the-art accuracy and complexity tradeoffs for inhomogeneous Poisson Process intensity estimation and multi-class kernel logistic regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge