Sparse Factor Analysis for Learning and Content Analytics
Paper and Code
Jul 19, 2013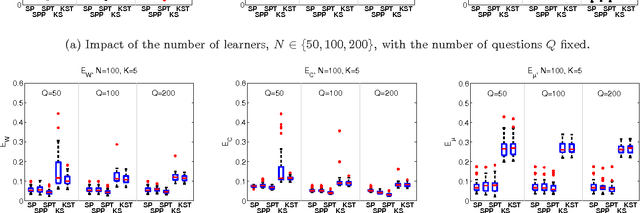
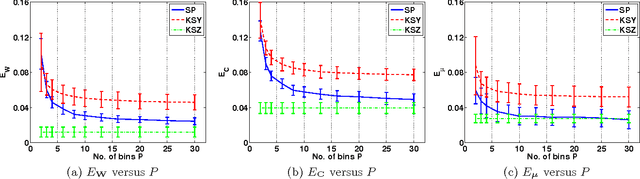
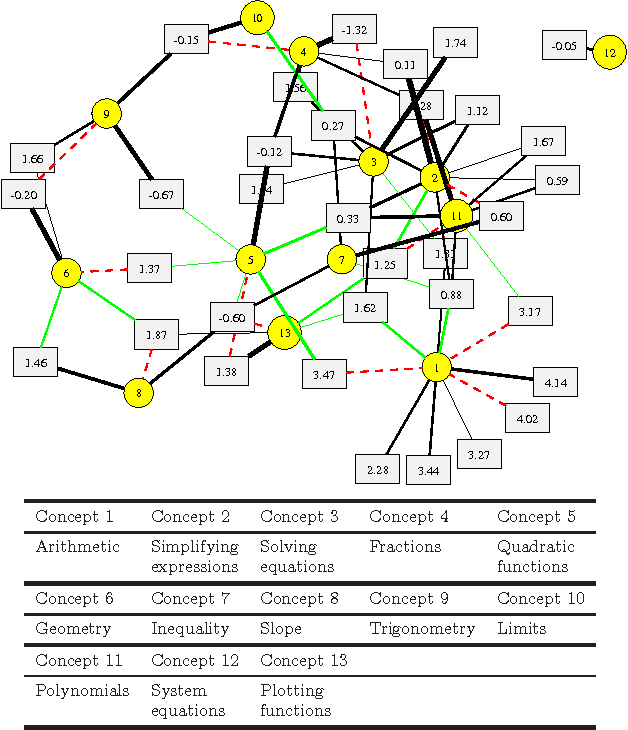
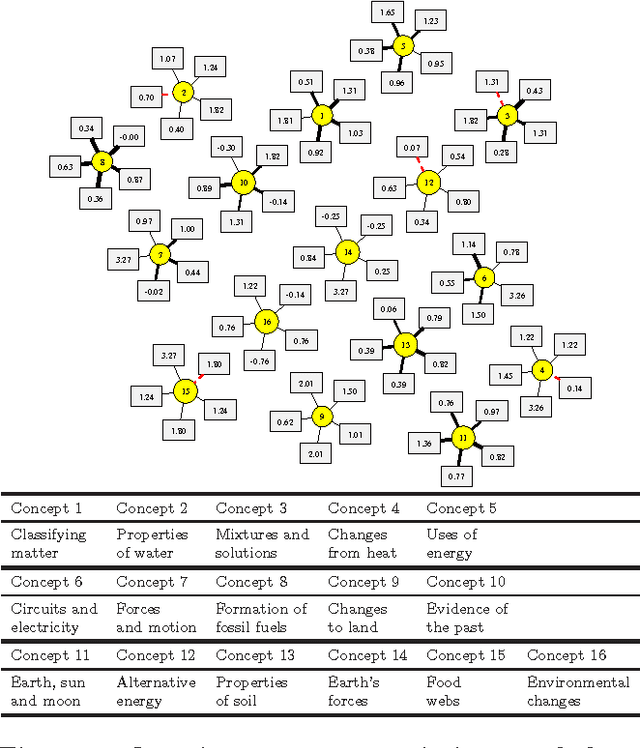
We develop a new model and algorithms for machine learning-based learning analytics, which estimate a learner's knowledge of the concepts underlying a domain, and content analytics, which estimate the relationships among a collection of questions and those concepts. Our model represents the probability that a learner provides the correct response to a question in terms of three factors: their understanding of a set of underlying concepts, the concepts involved in each question, and each question's intrinsic difficulty. We estimate these factors given the graded responses to a collection of questions. The underlying estimation problem is ill-posed in general, especially when only a subset of the questions are answered. The key observation that enables a well-posed solution is the fact that typical educational domains of interest involve only a small number of key concepts. Leveraging this observation, we develop both a bi-convex maximum-likelihood and a Bayesian solution to the resulting SPARse Factor Analysis (SPARFA) problem. We also incorporate user-defined tags on questions to facilitate the interpretability of the estimated factors. Experiments with synthetic and real-world data demonstrate the efficacy of our approach. Finally, we make a connection between SPARFA and noisy, binary-valued (1-bit) dictionary learning that is of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge