Sparse Compositional Metric Learning
Paper and Code
Apr 15, 2014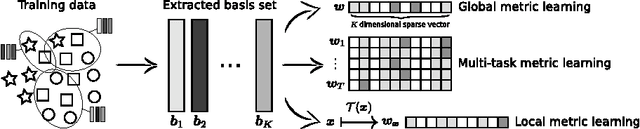
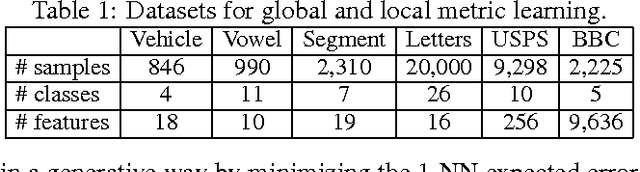
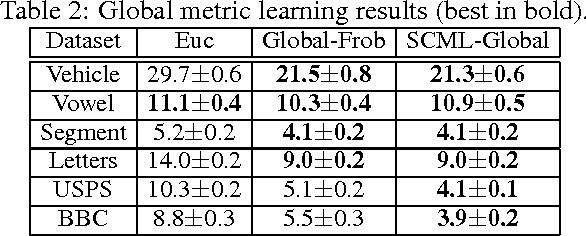
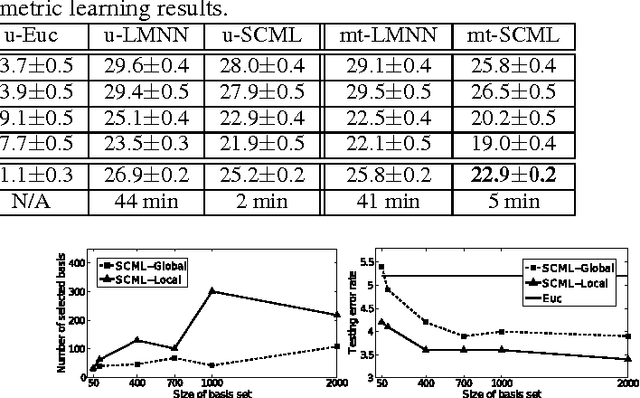
We propose a new approach for metric learning by framing it as learning a sparse combination of locally discriminative metrics that are inexpensive to generate from the training data. This flexible framework allows us to naturally derive formulations for global, multi-task and local metric learning. The resulting algorithms have several advantages over existing methods in the literature: a much smaller number of parameters to be estimated and a principled way to generalize learned metrics to new testing data points. To analyze the approach theoretically, we derive a generalization bound that justifies the sparse combination. Empirically, we evaluate our algorithms on several datasets against state-of-the-art metric learning methods. The results are consistent with our theoretical findings and demonstrate the superiority of our approach in terms of classification performance and scalability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge