Soft Conditional Computation

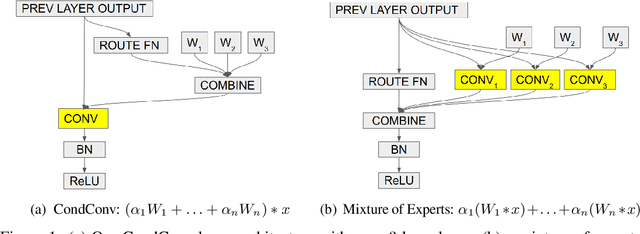
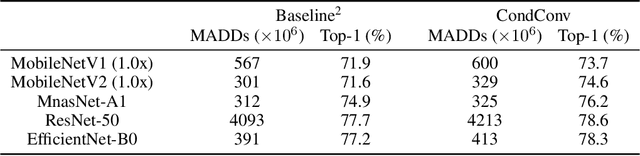
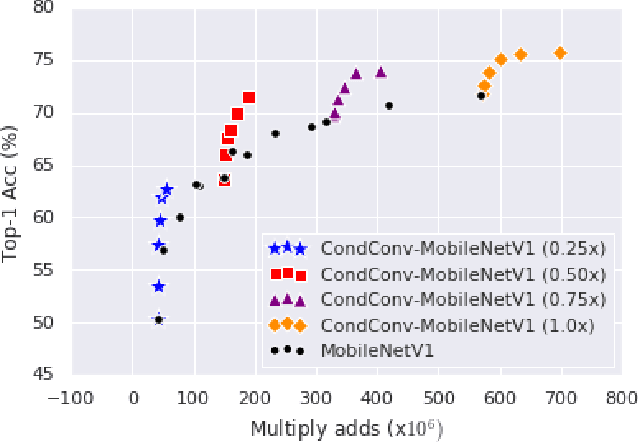
Conditional computation aims to increase the size and accuracy of a network, at a small increase in inference cost. Previous hard-routing models explicitly route the input to a subset of experts. We propose soft conditional computation, which, in contrast, utilizes all experts while still permitting efficient inference through parameter routing. Concretely, for a given convolutional layer, we wish to compute a linear combination of $n$ experts $\alpha_1 \cdot (W_1 * x) + \ldots + \alpha_n \cdot (W_n * x)$, where $\alpha_1, \ldots, \alpha_n$ are functions of the input learned through gradient descent. A straightforward evaluation requires $n$ convolutions. We propose an equivalent form of the above computation, $(\alpha_1 W_1 + \ldots + \alpha_n W_n) * x$, which requires only a single convolution. We demonstrate the efficacy of our method, named CondConv, by scaling up the MobileNetV1, MobileNetV2, and ResNet-50 model architectures to achieve higher accuracy while retaining efficient inference. On the ImageNet classification dataset, CondConv improves the top-1 validation accuracy of the MobileNetV1(0.5x) model from 63.8% to 71.6% while only increasing inference cost by 27%. On COCO object detection, CondConv improves the minival mAP of a MobileNetV1(1.0x) SSD model from 20.3 to 22.4 with just a 4% increase in inference cost.