Small Representations of Big Kidney Exchange Graphs
Paper and Code
Dec 16, 2016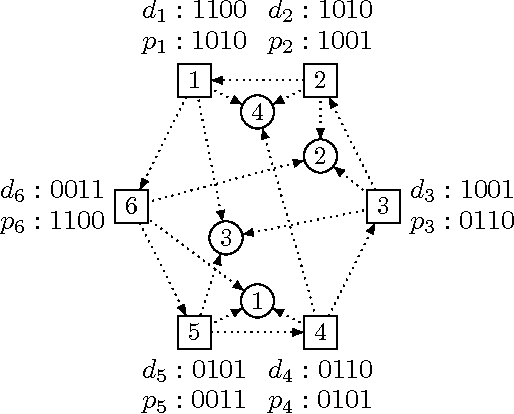
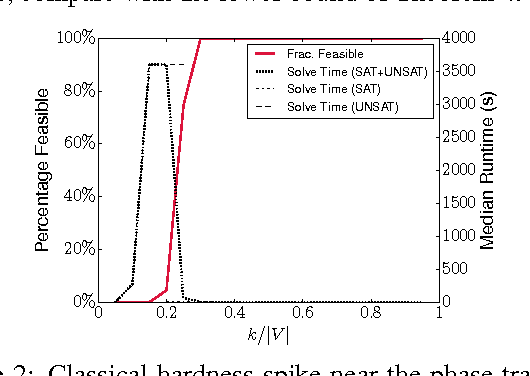
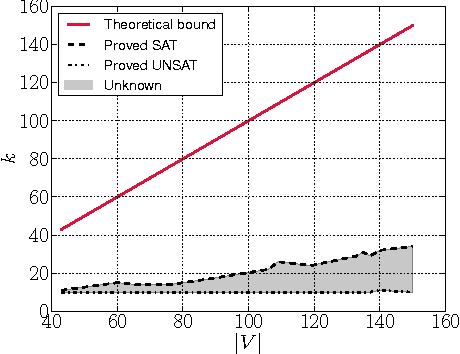

Kidney exchanges are organized markets where patients swap willing but incompatible donors. In the last decade, kidney exchanges grew from small and regional to large and national---and soon, international. This growth results in more lives saved, but exacerbates the empirical hardness of the $\mathcal{NP}$-complete problem of optimally matching patients to donors. State-of-the-art matching engines use integer programming techniques to clear fielded kidney exchanges, but these methods must be tailored to specific models and objective functions, and may fail to scale to larger exchanges. In this paper, we observe that if the kidney exchange compatibility graph can be encoded by a constant number of patient and donor attributes, the clearing problem is solvable in polynomial time. We give necessary and sufficient conditions for losslessly shrinking the representation of an arbitrary compatibility graph. Then, using real compatibility graphs from the UNOS nationwide kidney exchange, we show how many attributes are needed to encode real compatibility graphs. The experiments show that, indeed, small numbers of attributes suffice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge