Skewed Laplace Spectral Mixture kernels for long-term forecasting in Gaussian process

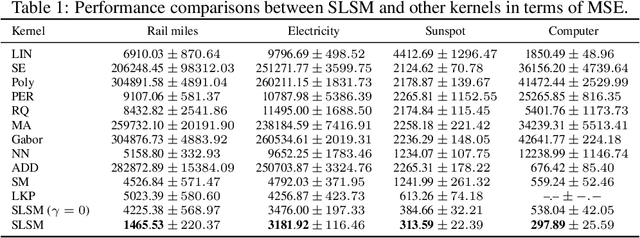
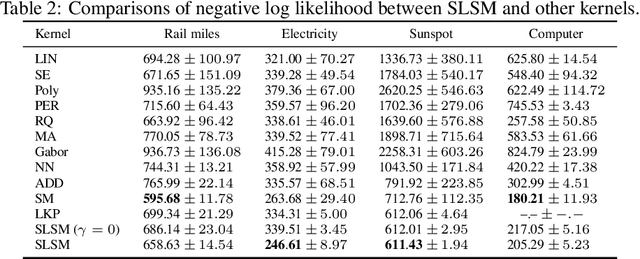
Long-term forecasting involves predicting a horizon that is far ahead of the last observation. It is a problem of highly practical relevance, for instance for companies in order to decide upon expensive long-term investments. Despite recent progress and success of Gaussian Processes (GPs) based on Spectral Mixture kernels, long-term forecasting remains a challenging problem for these kernels because they decay exponentially at large horizons. This is mainly due their use of a mixture of Gaussians to model spectral densities. The challenges underlying long-term forecasting become evident by investigating the distribution of the Fourier coefficients of (the training part of) the signal, which is non-smooth, heavy-tailed, sparse and skewed. Notably the heavy tail and skewness characteristics of such distribution in spectral domain allow to capture long range covariance of the signal in the time domain. Motivated by these observations, we propose to model spectral densities using a Skewed Laplace Spectral Mixture (SLSM) due to the skewness of its peaks, sparsity, non-smoothness, and heavy tail characteristics. By applying the inverse Fourier Transform to this spectral density we obtain a new GP kernel for long-term forecasting. Results of extensive experiments, including a multivariate time series, show the beneficial effect of the proposed SLSM kernel for long-term extrapolation and robustness to the choice of the number of mixture components.