Sigma Point Belief Propagation
Paper and Code
Nov 17, 2013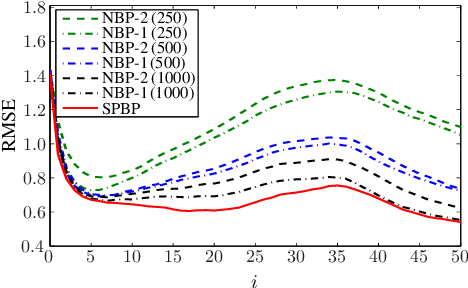
The sigma point (SP) filter, also known as unscented Kalman filter, is an attractive alternative to the extended Kalman filter and the particle filter. Here, we extend the SP filter to nonsequential Bayesian inference corresponding to loopy factor graphs. We propose sigma point belief propagation (SPBP) as a low-complexity approximation of the belief propagation (BP) message passing scheme. SPBP achieves approximate marginalizations of posterior distributions corresponding to (generally) loopy factor graphs. It is well suited for decentralized inference because of its low communication requirements. For a decentralized, dynamic sensor localization problem, we demonstrate that SPBP can outperform nonparametric (particle-based) BP while requiring significantly less computations and communications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge