Short and Wide Network Paths
Paper and Code
Nov 01, 2019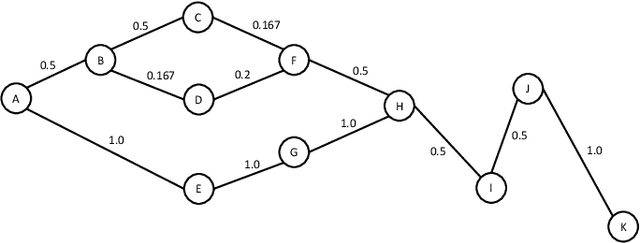

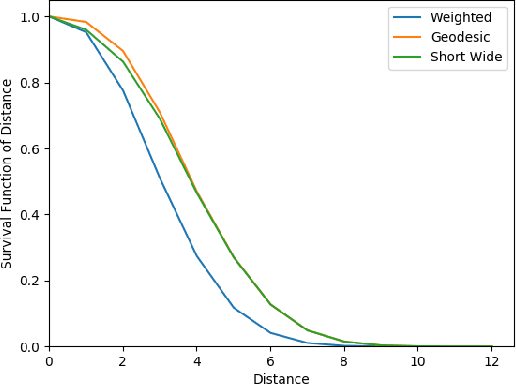
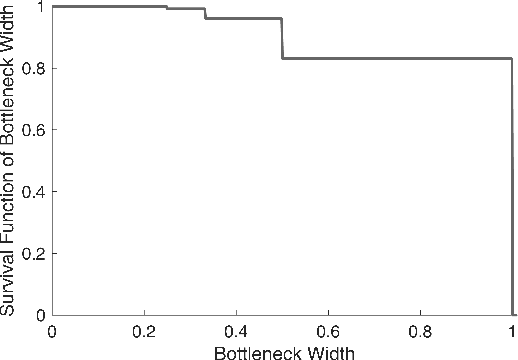
Network flow is a powerful mathematical framework to systematically explore the relationship between structure and function in biological, social, and technological networks. We introduce a new pipelining model of flow through networks where commodities must be transported over single paths rather than split over several paths and recombined. We show this notion of pipelined network flow is optimized using network paths that are both short and wide, and develop efficient algorithms to compute such paths for given pairs of nodes and for all-pairs. Short and wide paths are characterized for many real-world networks. To further demonstrate the utility of this network characterization, we develop novel information-theoretic lower bounds on computation speed in nervous systems due to limitations from anatomical connectivity and physical noise. For the nematode Caenorhabditis elegans, we find these bounds are predictive of biological timescales of behavior. Further, we find the particular C. elegans connectome is globally less efficient for information flow than random networks, but the hub-and-spoke architecture of functional subcircuits is optimal under constraint on number of synapses. This suggests functional subcircuits are a primary organizational principle of this small invertebrate nervous system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge