Shielded Decision-Making in MDPs
Paper and Code
Jul 16, 2018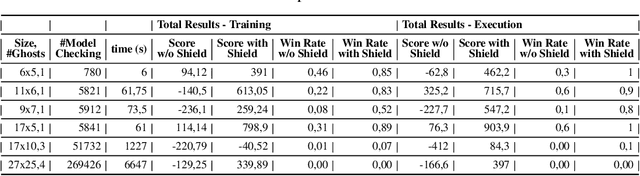
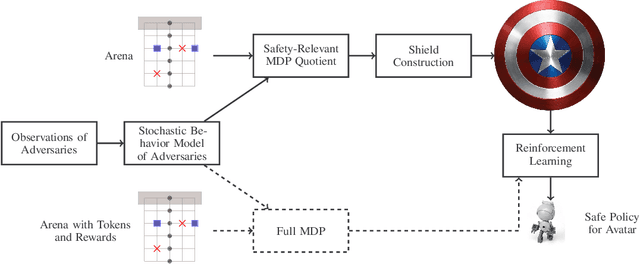
A prominent problem in artificial intelligence and machine learning is the safe exploration of an environment. In particular, reinforcement learning is a well-known technique to determine optimal policies for complicated dynamic systems, but suffers from the fact that such policies may induce harmful behavior. We present the concept of a shield that forces decision-making to provably adhere to safety requirements with high probability. Our method exploits the inherent uncertainties in scenarios given by Markov decision processes. We present a method to compute probabilities of decision making regarding temporal logic constraints. We use that information to realize a shield that---when applied to a reinforcement learning algorithm---ensures (near-)optimal behavior both for the safety constraints and for the actual learning objective. In our experiments, we show on the arcade game PAC-MAN that the learning efficiency increases as the learning needs orders of magnitude fewer episodes. We show tradeoffs between sufficient progress in exploration of the environment and ensuring strict safety.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge