Shapley Homology: Topological Analysis of Sample Influence for Neural Networks
Paper and Code
Oct 15, 2019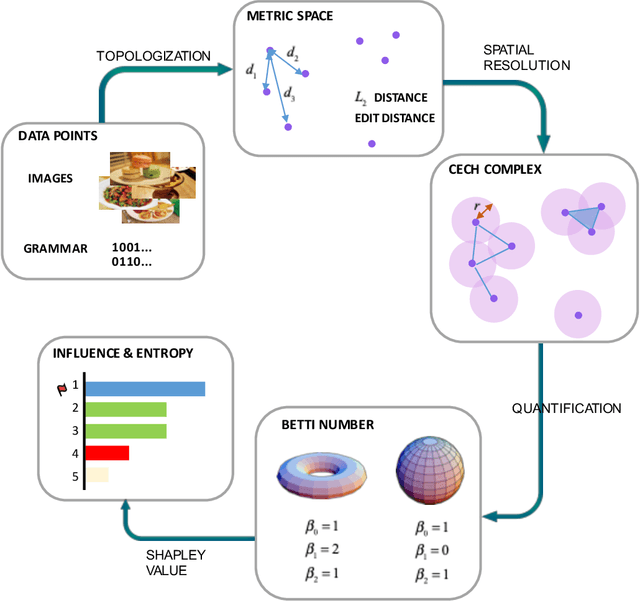

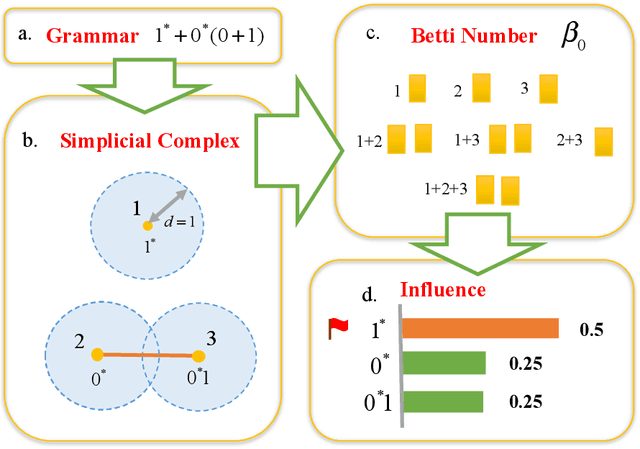
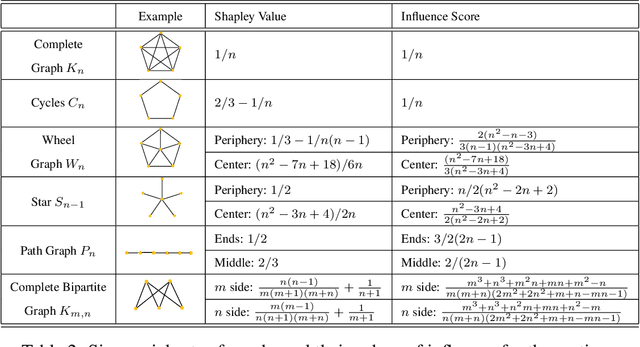
Data samples collected for training machine learning models are typically assumed to be independent and identically distributed (iid). Recent research has demonstrated that this assumption can be problematic as it simplifies the manifold of structured data. This has motivated different research areas such as data poisoning, model improvement, and explanation of machine learning models. In this work, we study the influence of a sample on determining the intrinsic topological features of its underlying manifold. We propose the Shapley Homology framework, which provides a quantitative metric for the influence of a sample of the homology of a simplicial complex. By interpreting the influence as a probability measure, we further define an entropy which reflects the complexity of the data manifold. Our empirical studies show that when using the 0-dimensional homology, on neighboring graphs, samples with higher influence scores have more impact on the accuracy of neural networks for determining the graph connectivity and on several regular grammars whose higher entropy values imply more difficulty in being learned.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge