Sequential Controlled Sensing for Composite Multihypothesis Testing
Paper and Code
Oct 24, 2019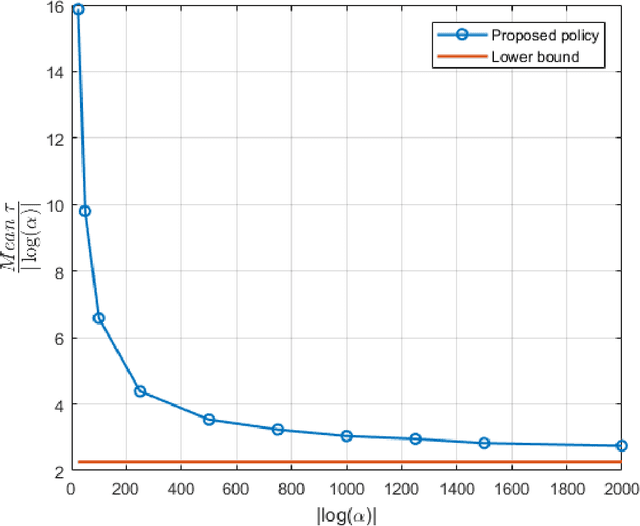
The problem of multi-hypothesis testing with controlled sensing of observations is considered. The distribution of observations collected under each control is assumed to follow a single-parameter exponential family distribution. The goal is to design a policy to find the true hypothesis with minimum expected delay while ensuring that the probability of error is below a given constraint. The decision-maker can control the delay by intelligently choosing the control for observation collection in each time slot. We derive a policy that satisfies the given constraint on the error probability. We also show that the policy is asymptotically optimal in the sense that it asymptotically achieves an information-theoretic lower bound on the expected delay.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge