Sequential algorithmic modification with test data reuse
Paper and Code
Mar 21, 2022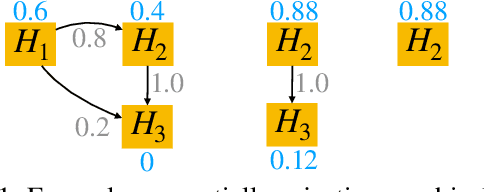
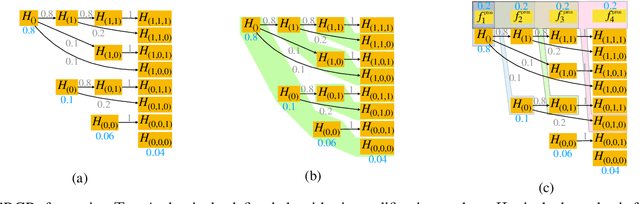
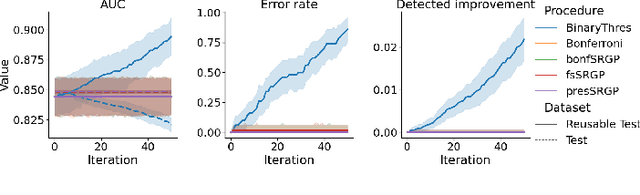
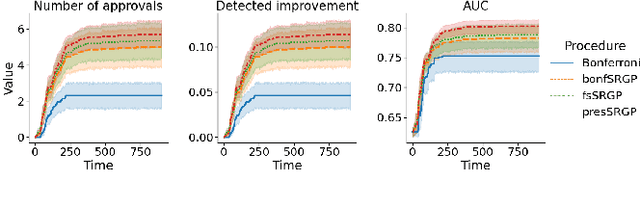
After initial release of a machine learning algorithm, the model can be fine-tuned by retraining on subsequently gathered data, adding newly discovered features, or more. Each modification introduces a risk of deteriorating performance and must be validated on a test dataset. It may not always be practical to assemble a new dataset for testing each modification, especially when most modifications are minor or are implemented in rapid succession. Recent works have shown how one can repeatedly test modifications on the same dataset and protect against overfitting by (i) discretizing test results along a grid and (ii) applying a Bonferroni correction to adjust for the total number of modifications considered by an adaptive developer. However, the standard Bonferroni correction is overly conservative when most modifications are beneficial and/or highly correlated. This work investigates more powerful approaches using alpha-recycling and sequentially-rejective graphical procedures (SRGPs). We introduce novel extensions that account for correlation between adaptively chosen algorithmic modifications. In empirical analyses, the SRGPs control the error rate of approving unacceptable modifications and approve a substantially higher number of beneficial modifications than previous approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge