Sensing-Aware Kernel SVM
Paper and Code
Mar 13, 2014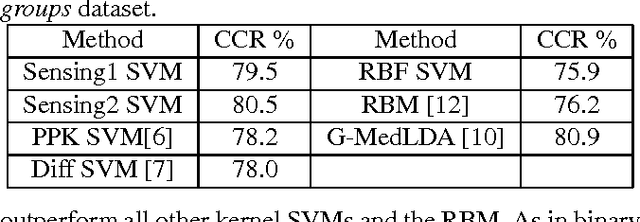
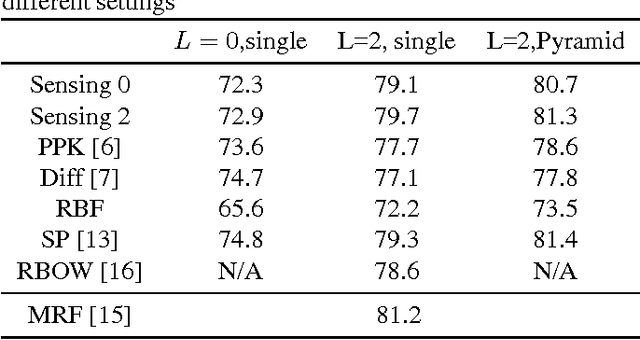
We propose a novel approach for designing kernels for support vector machines (SVMs) when the class label is linked to the observation through a latent state and the likelihood function of the observation given the state (the sensing model) is available. We show that the Bayes-optimum decision boundary is a hyperplane under a mapping defined by the likelihood function. Combining this with the maximum margin principle yields kernels for SVMs that leverage knowledge of the sensing model in an optimal way. We derive the optimum kernel for the bag-of-words (BoWs) sensing model and demonstrate its superior performance over other kernels in document and image classification tasks. These results indicate that such optimum sensing-aware kernel SVMs can match the performance of rather sophisticated state-of-the-art approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge