Semi-supervised lane detection with Deep Hough Transform
Paper and Code
Jun 09, 2021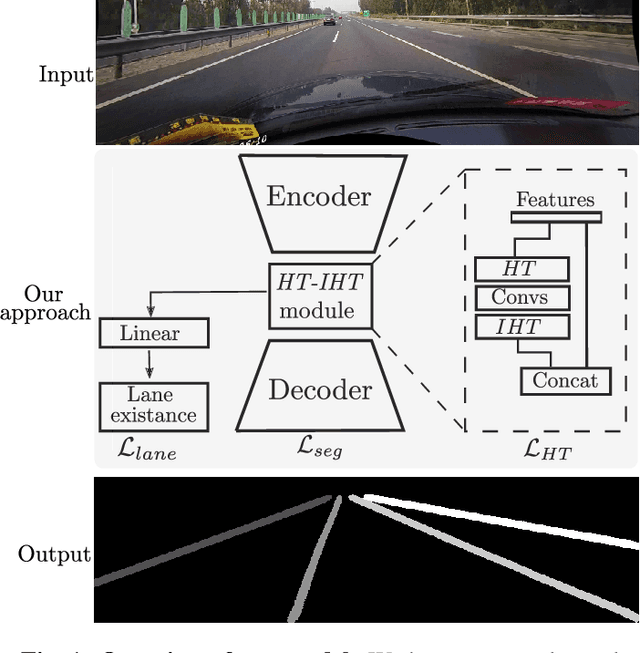
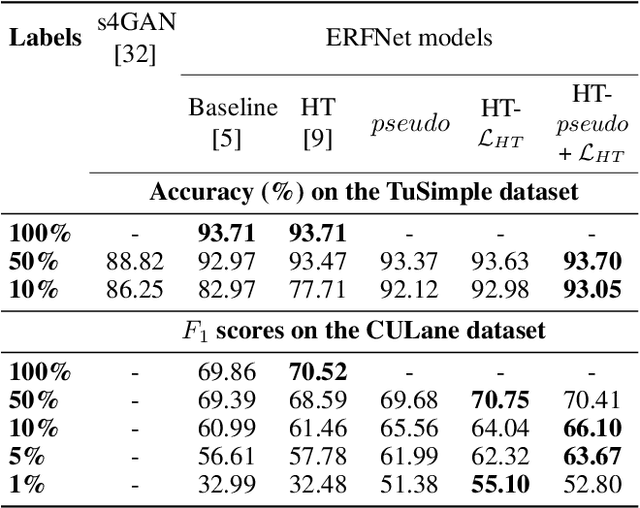

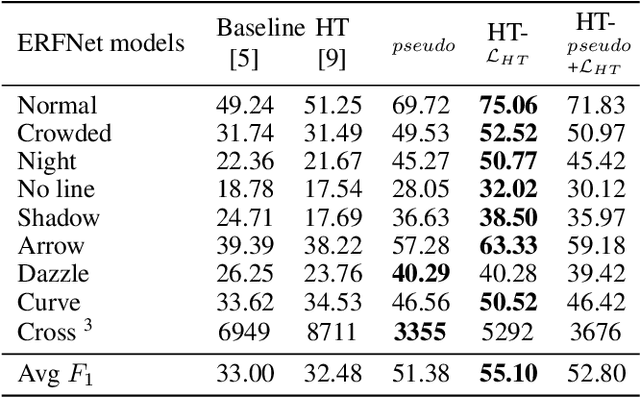
Current work on lane detection relies on large manually annotated datasets. We reduce the dependency on annotations by leveraging massive cheaply available unlabelled data. We propose a novel loss function exploiting geometric knowledge of lanes in Hough space, where a lane can be identified as a local maximum. By splitting lanes into separate channels, we can localize each lane via simple global max-pooling. The location of the maximum encodes the layout of a lane, while the intensity indicates the the probability of a lane being present. Maximizing the log-probability of the maximal bins helps neural networks find lanes without labels. On the CULane and TuSimple datasets, we show that the proposed Hough Transform loss improves performance significantly by learning from large amounts of unlabelled images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge