Semi-supervised Dictionary Learning Based on Hilbert-Schmidt Independence Criterion
Paper and Code
Apr 25, 2016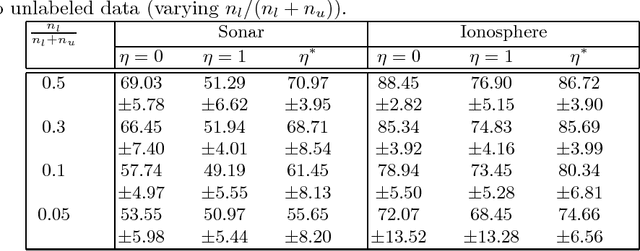
In this paper, a novel semi-supervised dictionary learning and sparse representation (SS-DLSR) is proposed. The proposed method benefits from the supervisory information by learning the dictionary in a space where the dependency between the data and class labels is maximized. This maximization is performed using Hilbert-Schmidt independence criterion (HSIC). On the other hand, the global distribution of the underlying manifolds were learned from the unlabeled data by minimizing the distances between the unlabeled data and the corresponding nearest labeled data in the space of the dictionary learned. The proposed SS-DLSR algorithm has closed-form solutions for both the dictionary and sparse coefficients, and therefore does not have to learn the two iteratively and alternately as is common in the literature of the DLSR. This makes the solution for the proposed algorithm very fast. The experiments confirm the improvement in classification performance on benchmark datasets by including the information from both labeled and unlabeled data, particularly when there are many unlabeled data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge