Semi-Counterfactual Risk Minimization Via Neural Networks

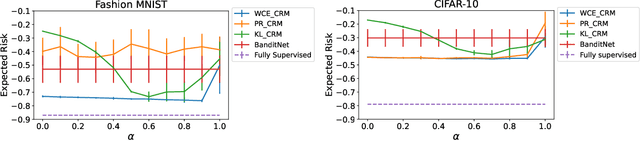
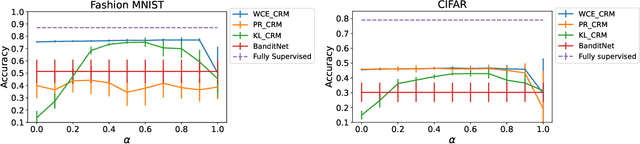
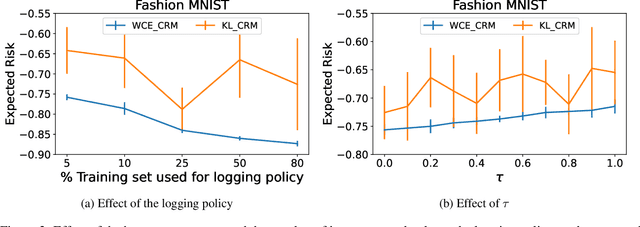
Counterfactual risk minimization is a framework for offline policy optimization with logged data which consists of context, action, propensity score, and reward for each sample point. In this work, we build on this framework and propose a learning method for settings where the rewards for some samples are not observed, and so the logged data consists of a subset of samples with unknown rewards and a subset of samples with known rewards. This setting arises in many application domains, including advertising and healthcare. While reward feedback is missing for some samples, it is possible to leverage the unknown-reward samples in order to minimize the risk, and we refer to this setting as semi-counterfactual risk minimization. To approach this kind of learning problem, we derive new upper bounds on the true risk under the inverse propensity score estimator. We then build upon these bounds to propose a regularized counterfactual risk minimization method, where the regularization term is based on the logged unknown-rewards dataset only; hence it is reward-independent. We also propose another algorithm based on generating pseudo-rewards for the logged unknown-rewards dataset. Experimental results with neural networks and benchmark datasets indicate that these algorithms can leverage the logged unknown-rewards dataset besides the logged known-reward dataset.