Search-based Motion Planning for Quadrotors using Linear Quadratic Minimum Time Control
Paper and Code
Sep 15, 2017
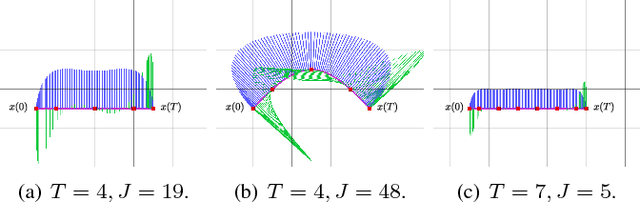
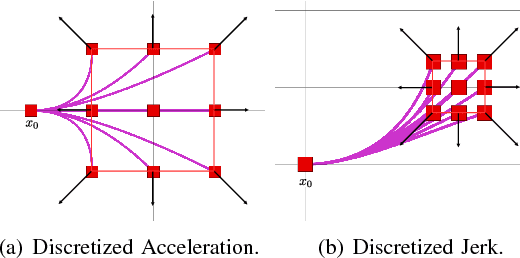
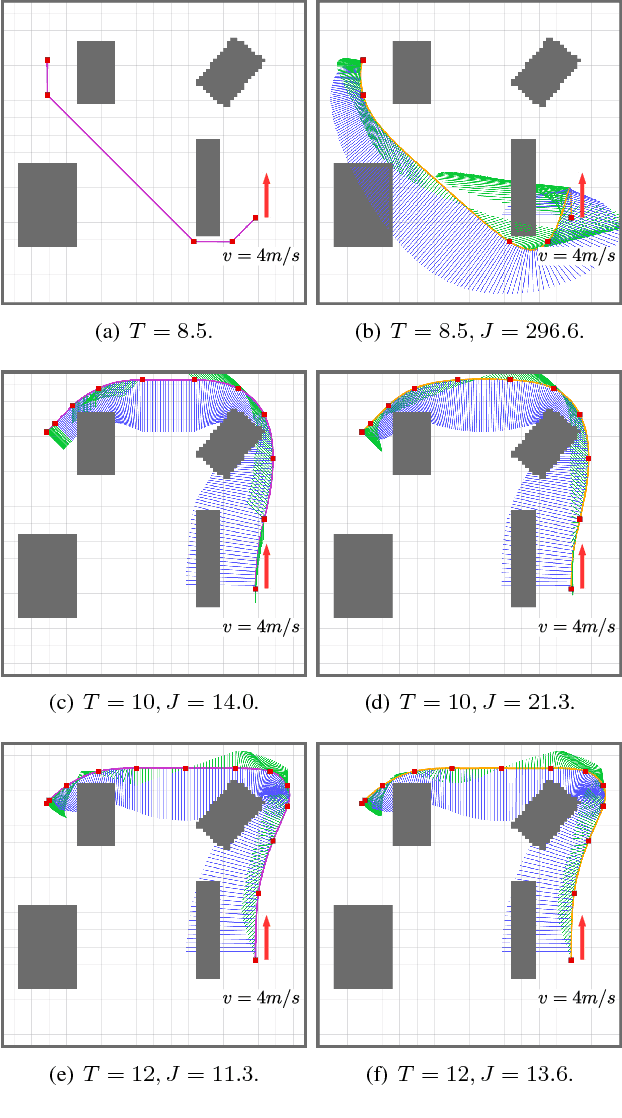
In this work, we propose a search-based planning method to compute dynamically feasible trajectories for a quadrotor flying in an obstacle-cluttered environment. Our approach searches for smooth, minimum-time trajectories by exploring the map using a set of short-duration motion primitives. The primitives are generated by solving an optimal control problem and induce a finite lattice discretization on the state space which can be explored using a graph-search algorithm. The proposed approach is able to generate resolution-complete (i.e., optimal in the discretized space), safe, dynamically feasibility trajectories efficiently by exploiting the explicit solution of a Linear Quadratic Minimum Time problem. It does not assume a hovering initial condition and, hence, is suitable for fast online re-planning while the robot is moving. Quadrotor navigation with online re-planning is demonstrated using the proposed approach in simulation and physical experiments and comparisons with trajectory generation based on state-of-art quadratic programming are presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge