Score-Based Generative Modeling through Stochastic Differential Equations
Paper and Code
Nov 26, 2020
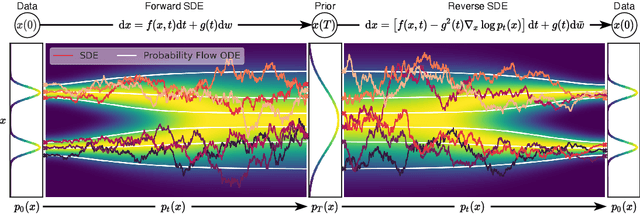

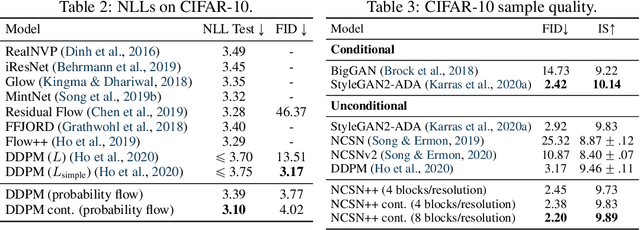
Creating noise from data is easy; creating data from noise is generative modeling. We present a stochastic differential equation (SDE) that smoothly transforms a complex data distribution to a known prior distribution by slowly injecting noise, and a corresponding reverse-time SDE that transforms the prior distribution back into the data distribution by slowly removing the noise. Crucially, the reverse-time SDE depends only on the time-dependent gradient field (a.k.a., score) of the perturbed data distribution. By leveraging advances in score-based generative modeling, we can accurately estimate these scores with neural networks, and use numerical SDE solvers to generate samples. We show that this framework encapsulates previous approaches in diffusion probabilistic modeling and score-based generative modeling, and allows for new sampling procedures. In particular, we introduce a predictor-corrector framework to correct errors in the evolution of the discretized reverse-time SDE. We also derive an equivalent neural ODE that samples from the same distribution as the SDE, which enables exact likelihood computation, and improved sampling efficiency. In addition, our framework enables conditional generation with an unconditional model, as we demonstrate with experiments on class-conditional generation, image inpainting, and colorization. Combined with multiple architectural improvements, we achieve record-breaking performance for unconditional image generation on CIFAR-10 with an Inception score of 9.89 and FID of 2.20, a competitive likelihood of 3.10 bits/dim, and demonstrate high fidelity generation of $1024 \times 1024$ images for the first time from a score-based generative model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge