Scalable Gaussian Process Classification with Additive Noise for Various Likelihoods
Paper and Code
Sep 14, 2019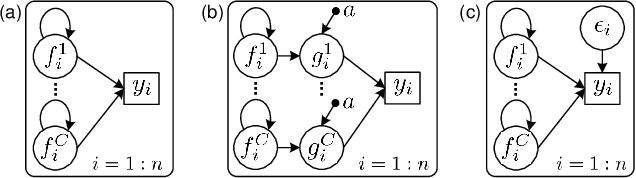
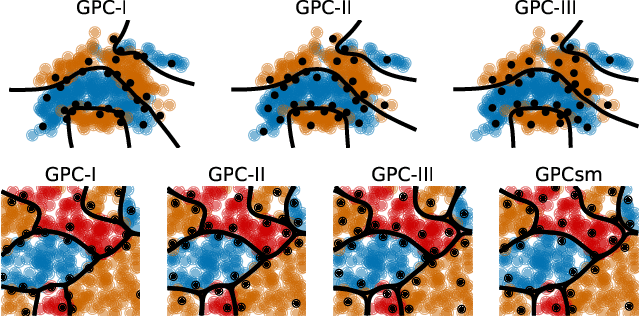
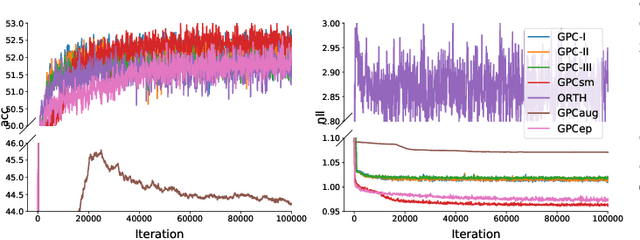
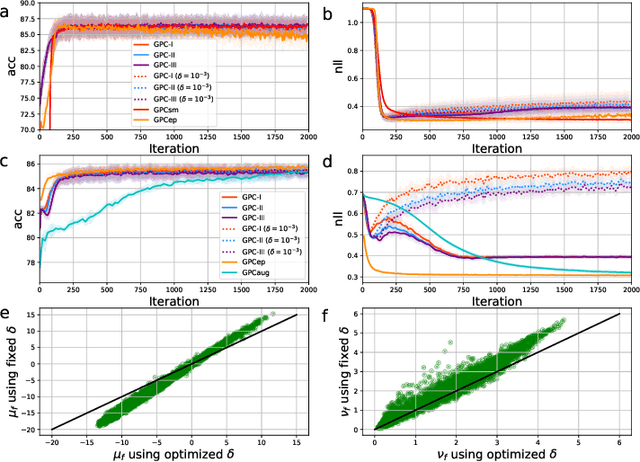
Gaussian process classification (GPC) provides a flexible and powerful statistical framework describing joint distributions over function space. Conventional GPCs however suffer from (i) poor scalability for big data due to the full kernel matrix, and (ii) intractable inference due to the non-Gaussian likelihoods. Hence, various scalable GPCs have been proposed through (i) the sparse approximation built upon a small inducing set to reduce the time complexity; and (ii) the approximate inference to derive analytical evidence lower bound (ELBO). However, these scalable GPCs equipped with analytical ELBO are limited to specific likelihoods or additional assumptions. In this work, we present a unifying framework which accommodates scalable GPCs using various likelihoods. Analogous to GP regression (GPR), we introduce additive noises to augment the probability space for (i) the GPCs with step, (multinomial) probit and logit likelihoods via the internal variables; and particularly, (ii) the GPC using softmax likelihood via the noise variables themselves. This leads to unified scalable GPCs with analytical ELBO by using variational inference. Empirically, our GPCs showcase better results than state-of-the-art scalable GPCs for extensive binary/multi-class classification tasks with up to two million data points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge