Scalable Distributional Robustness in a Class of Non Convex Optimization with Guarantees
Paper and Code
May 31, 2022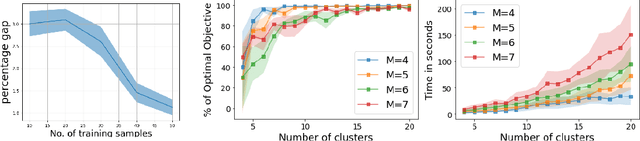
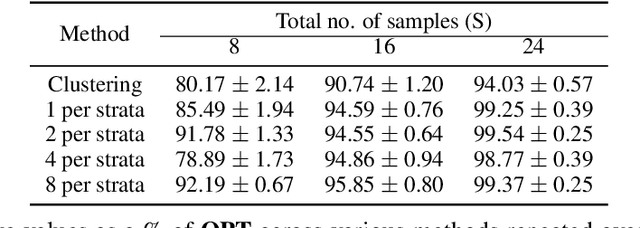


Distributionally robust optimization (DRO) has shown lot of promise in providing robustness in learning as well as sample based optimization problems. We endeavor to provide DRO solutions for a class of sum of fractionals, non-convex optimization which is used for decision making in prominent areas such as facility location and security games. In contrast to previous work, we find it more tractable to optimize the equivalent variance regularized form of DRO rather than the minimax form. We transform the variance regularized form to a mixed-integer second order cone program (MISOCP), which, while guaranteeing near global optimality, does not scale enough to solve problems with real world data-sets. We further propose two abstraction approaches based on clustering and stratified sampling to increase scalability, which we then use for real world data-sets. Importantly, we provide near global optimality guarantees for our approach and show experimentally that our solution quality is better than the locally optimal ones achieved by state-of-the-art gradient-based methods. We experimentally compare our different approaches and baselines, and reveal nuanced properties of a DRO solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge