Sampling Theorems for Learning from Incomplete Measurements
Paper and Code
Jan 31, 2022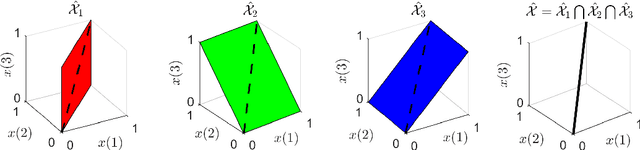

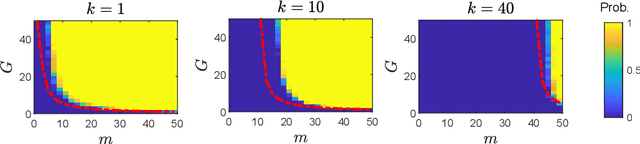
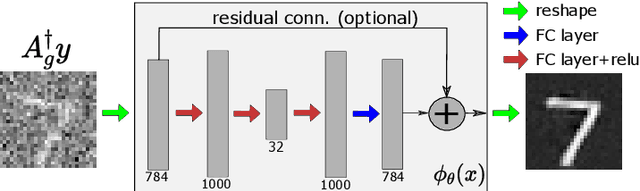
In many real-world settings, only incomplete measurement data are available which can pose a problem for learning. Unsupervised learning of the signal model using a fixed incomplete measurement process is impossible in general, as there is no information in the nullspace of the measurement operator. This limitation can be overcome by using measurements from multiple operators. While this idea has been successfully applied in various applications, a precise characterization of the conditions for learning is still lacking. In this paper, we fill this gap by presenting necessary and sufficient conditions for learning the signal model which indicate the interplay between the number of distinct measurement operators $G$, the number of measurements per operator $m$, the dimension of the model $k$ and the dimension of the signals $n$. In particular, we show that generically unsupervised learning is possible if each operator obtains at least $m>k+n/G$ measurements. Our results are agnostic of the learning algorithm and have implications in a wide range of practical algorithms, from low-rank matrix recovery to deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge