Sampling-Based Motion Planning on Manifold Sequences

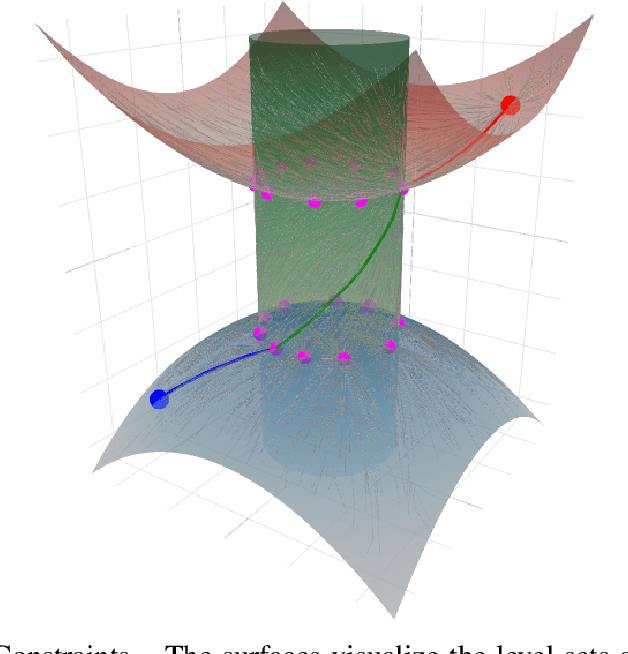
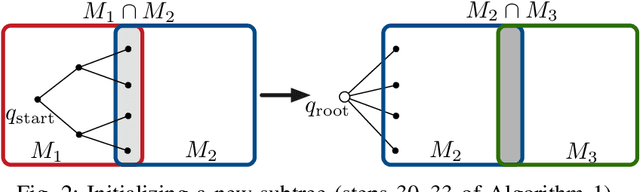
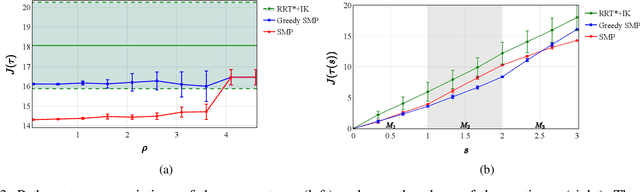
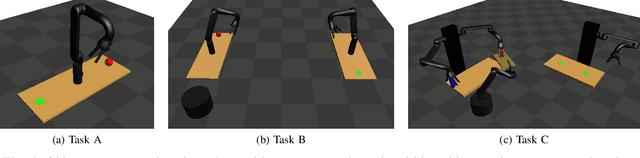
We address the problem of planning robot motions in constrained configuration spaces where the constraints change throughout the motion. A novel problem formulation is introduced that describes a task as a sequence of intersecting manifolds, which the robot needs to traverse in order to solve the task. We specify a class of sequential motion planning problems that fulfill a particular property of the change in the free configuration space when transitioning between manifolds. For this problem class, a sequential motion planning algorithm SMP is developed that searches for optimal intersection points between manifolds by using RRT* in an inner loop with a novel steering strategy. We provide a theoretical analysis regarding its probabilistic completeness and demonstrate its performance on kinematic planning problems where the constraints are represented as geometric primitives. Further, we show its capabilities on solving multi-robot object transportation tasks.