Sample Complexity Bounds for Recurrent Neural Networks with Application to Combinatorial Graph Problems
Paper and Code
Jan 29, 2019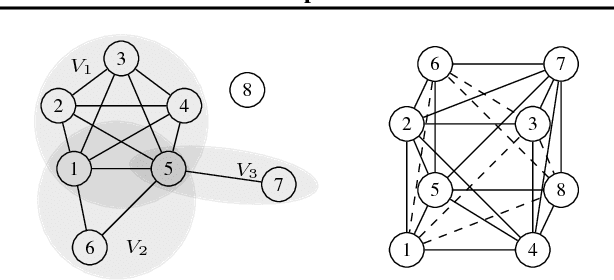
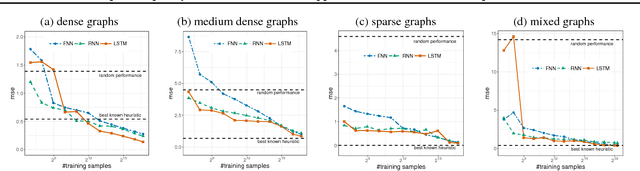
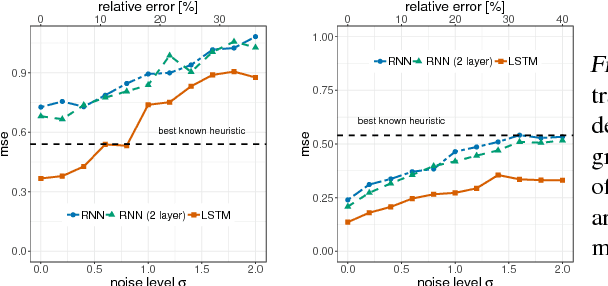
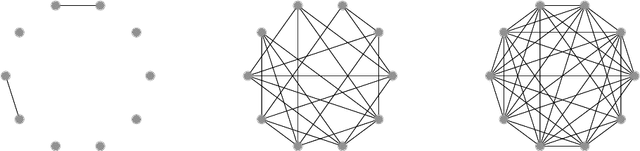
Learning to predict solutions to real-valued combinatorial graph problems promises efficient approximations. As demonstrated based on the NP-hard edge clique cover number, recurrent neural networks (RNNs) are particularly suited for this task and can even outperform state-of-the-art heuristics. However, the theoretical framework for estimating real-valued RNNs is understood only poorly. As our primary contribution, this is the first work that upper bounds the sample complexity for learning real-valued RNNs. While such derivations have been made earlier for feed-forward and convolutional neural networks, our work presents the first such attempt for recurrent neural networks. Given a single-layer RNN with $a$ rectified linear units and input of length $b$, we show that a population prediction error of $\varepsilon$ can be realized with at most $\tilde{\mathcal{O}}(a^4b/\varepsilon^2)$ samples. We further derive comparable results for multi-layer RNNs. Accordingly, a size-adaptive RNN fed with graphs of at most $n$ vertices can be learned in $\tilde{\mathcal{O}}(n^6/\varepsilon^2)$, i.e., with only a polynomial number of samples. For combinatorial graph problems, this provides a theoretical foundation that renders RNNs competitive.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge